Práctica 4: Convolución y Correlación de señales

Simulación numérica de convolución
Correlación númerica
Convolución de señales en tiempo discreto
Correlación de señales en tiempo discreto
Entregables

Simulación numérica de convolución

Existen diferentes formas de implementar simulaciones numéricas de convoluciones. De acuerdo a la definición matemática de convolución necesitamos resolver una integral de una multiplicación de señales, entonces implementar una simulación de convolución se subdivide en entender que significa integrar numéricamente y posteriormente elegir un algoritmo que resuelva el problema de integración.

La siguiente lista de reproducción explica sobre la simulación numérica de integrales, no se explican todos los algoritmos exitentes (hay bastantes) pero sirve para tener una idea de lo que se busca en general cuando se realizan simulaciones numericas

Para la implementación númerica es importante tener en cuenta la duración de cada señal, recuerde que es imposible hacer simulaciones númericas que involucren cantidades infinitas. Si una señal tiene duración 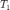$T_1$ y otra señal 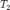$T_2$ la convolución tendrá duración $T_1+T_2$ ; donde la duración se refiere al intervalo para el cual la señal no es totalmente cero.

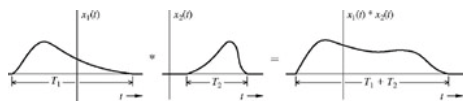
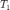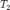Cabe señalar que si las señales involucradas tienen duración infinita podría elegirse $T_1$ y $T_2$ lo suficientemente grande para tener una idea de lo que sucede con el resultado de su convolución

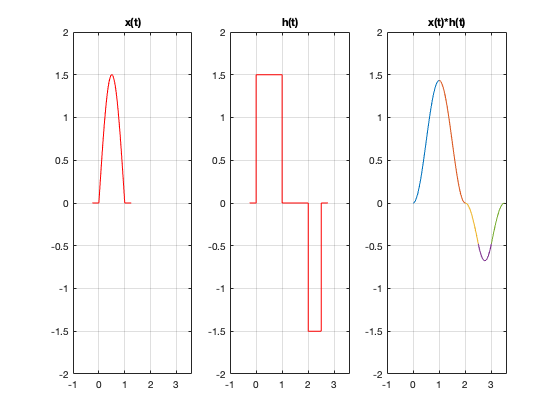
Por ejemplo si queremos realizar la convolución de las siguientes señales

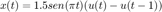
$x(t)=1.5sen(\pi t)(u(t)-u(t-1))$

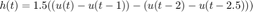
$$h(t)=1.5((u(t)-u(t-1))-(u(t-2)-u(t-2.5)))$$

la señal resultante tendrá longitud de 3.5.

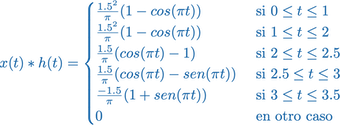
Ahora se pueden implementar la grafica en MATLAB,

figure
subplot(1,3,1)
syms t
x=piecewise(t<0,0,0<t<1,1.5*sin(pi*t),t>1,0);
fplot(x,[-0.25,1.25],'r')
grid on
title('x(t)')
axis([-1 3.6 -2 2]);
subplot(1,3,2)
h=piecewise(t<0,0,0<t<1,1.5,1<t<2,0,2<t<2.5,-1.5,t>2.5,0);
fplot(h,[-0.25,2.75],'r')
grid on
title('h(t)')
axis([-1 3.6 -2 2]);
t1=0:0.01:1;
t2=1:0.01:2;
t3=2:0.01:2.5;
t4=2.5:0.01:3;
t5=3:0.01:3.5;
subplot(1,3,3)
plot(t1,(1.5^2/pi)*(1-cos(pi*t1)))
hold on
plot(t2,(1.5^2/pi)*(1-cos(pi*t2)))
plot(t3,(1.5/pi)*(cos(pi*t3)-1))
plot(t4,(1.5/pi)*(cos(pi*t4)-sin(pi*t4)))
plot(t5, (-1.5/pi)*(1+sin(pi*t5)))
grid on
title('x(t)*h(t)')
axis([-1 3.6 -2 2]);

El siguiente código es una modificación del código de Lathi (Código del capítulo 2, M2.4 pág 161), ejemplo de convoluciones continuas

  function convconm(x,h)
  figure (1) % Se crea una figura para hacer las gráficas
  dtau = 0.005; % Base de los rectangulos para realizar la integral 
  tau = -1:dtau:4; % Intervalo de visualización del resultado
  ti = 0; % Indice para el vector de resultados
  tvec = -.25:.1:3.75; % traslaciones de t, cuantas integrales se calulan  
  y = NaN*zeros(1, length (tvec)); % Resultados de acuerdo a cuantos t
  for t = tvec, % Cantidad de traslaciones
      ti = ti+1; % Indice para guardar el resultado (indice del tiempo)
      xh = x(t-tau).*h(tau); % resultado de la multiplicación 
      lxh = length(xh); % longitud del resultado
      y(ti) = sum(xh.*dtau); % Base por altura, aproximación de la integral
      subplot (2,1,1), % gráfica de 2 x 1 (primera)
      plot(tau, h(tau), 'r-', tau, x(t-tau), 'g--', t, 0, 'ob'); %graficas 
      axis ([tau(1) tau(end) -2.0 2.5]); % límites de los ejes
      patch([tau(1:end-1); tau(1:end-1); tau(2:end); tau(2:end)],...
      [zeros(1,lxh-1);xh(1:end-1);xh(2:end);zeros(1,lxh-1)],...
      [.8 .8 .8], 'edgecolor', 'none');
      xlabel('\tau'); % Texto del eje X
      legend('h(\tau)', 'x(t-\tau)','t','h(\tau)x(t-\tau)')% Caja de Texto  
      subplot (2, 1, 2)  % gráfica de 2 x 1 (segunda)
      plot (tvec, y, 'k', tvec (ti), y(ti), 'ok');
      xlabel ('t'); 
      ylabel ('y(t) = \int h(\tau)x(t-\tau) d\tau');
      axis ([tau(1) tau(end) -1.0 2.0]); % límites del eje
      grid; % malla
      drawnow; % efecto de movimiento continuo
  end
  end

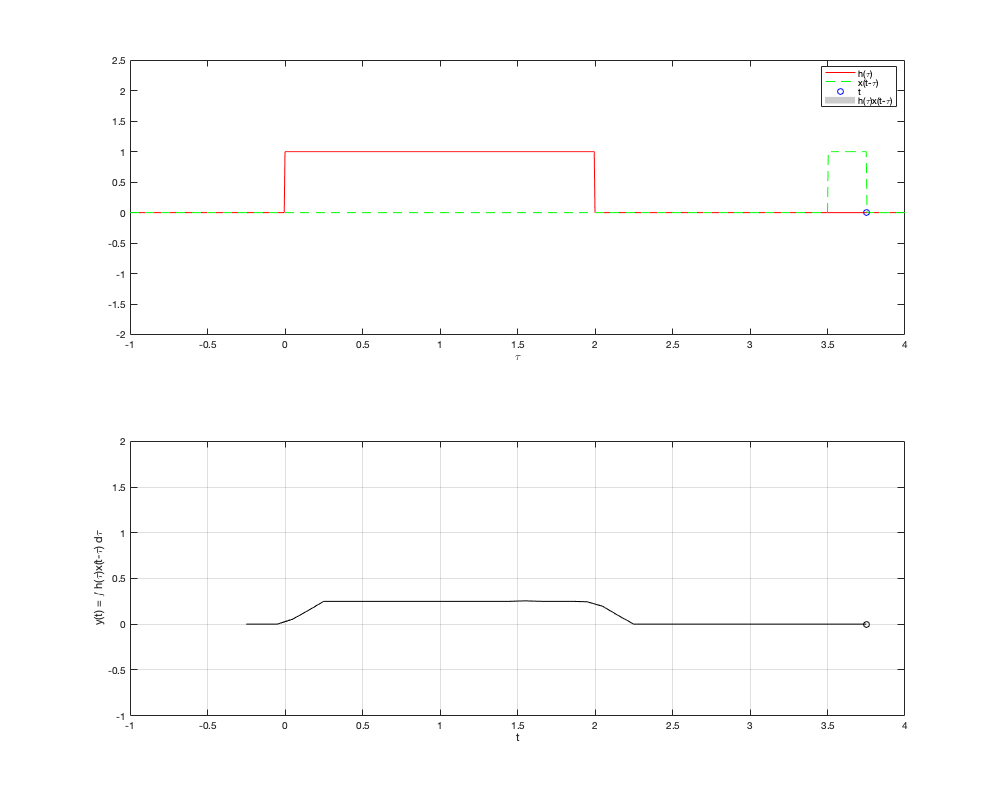
Si ejecutamos las siguientes instrucciones en el Command Window y el directorio de trabajo es el mismo donde se encuentra la función convconm tendrémos el siguiente resultado

x = @(t) 1.5*sin(pi*t).*(t>=0 & t<1);
h = @(t) 1.5*((t>=0&t<1.0) - (t>=2&t<2.5));
convconm(x,h)

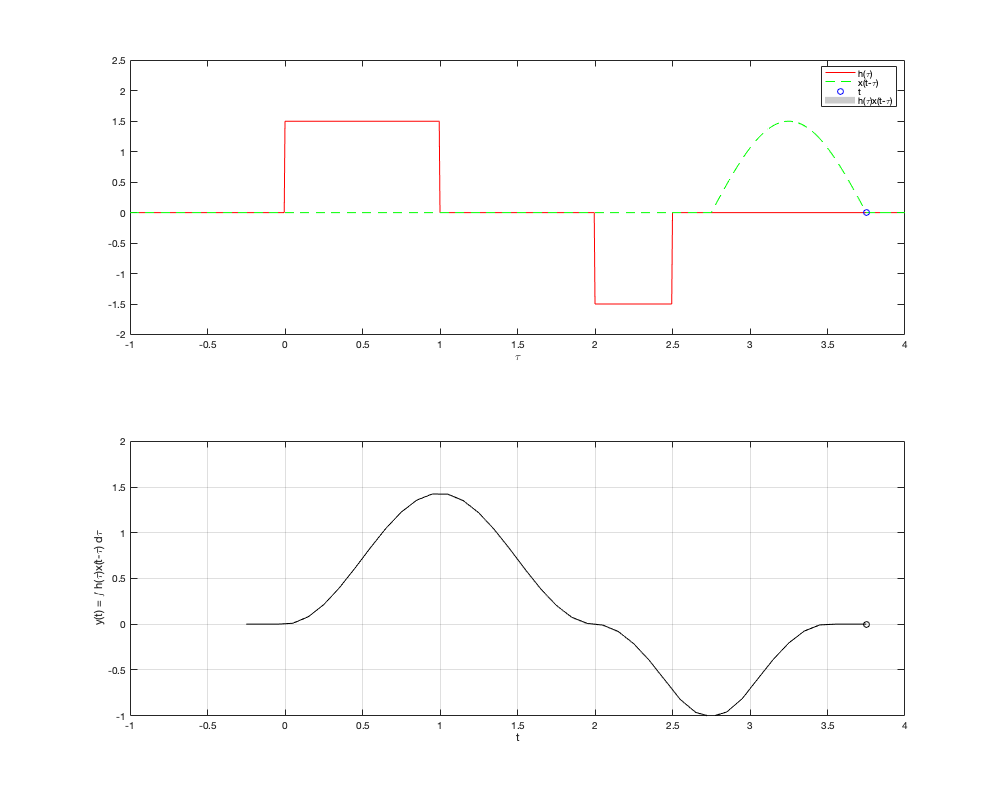
El cual puede compararse con la gráfica del resultado análitico y observar que la solución númerica es una buena aproximación de la exacta.

Correlación númerica

Una manera de abordar este problema es recordando una equivalencia de la correlación

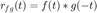
$r_{fg}(t)=f(t)*g(-t)$

Entonces por ejemplo si se quisiera realizar la correlación de las señales

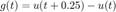
$$g(t)=u(t+0.25)-u(t)$$

$$f(t)=u(t)-u(t-2)$$

El código de convolución podría ocuparse de la siguiente manera

g = @(t) (t>=0 & t<0.25);
f = @(t) (t>=0&t<2);
convconm(g,f)

Convolución de señales en tiempo discreto

La convolución de señales en tiempo discreto da como resultado otra señal en tiempo discreto, la operación se define como

$x_3[n]=\sum_{m=-\infty}^\infty x_1[m]x_2[n-m]$

Mediante calculos computacionales directos no podemos obtener el resultado para señales de longitud infinita, por lo que acotaremos nuestra descripción a señales causales de longitud finita, para ello daremos algunas anotaciones para considerar en nuestro algoritmo

Si la señal tiene longitu 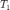y la señal tiene longitud 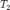entonces la señal 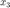tiene longitud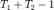
La instrucción conv de MATLAB ayuda a calcular las convoluciones, hay que tener cuidado con las especificaciones, consultar Lathi capítulo 3 sección M3.4

function convdisc(x1,x2)
    Tam1 = size(x1(1,:));
    Tam2 = size(x2(1,:));
    T1 = Tam1(2);
    T2 = Tam2(2);
    T3 = T1+T2-1;
    vec1 = zeros(1,T1+2*T2-2);
    vec2 = zeros(1,T1+2*T2-2);
    Tec2 = -(T2-1):(T1+T2-2);
    size(vec2);
    size(Tec2);
    x3=zeros(2,T3);
    x3(1,:)=0:T3-1;
    x3(1,:)=x3(1,:)+x1(1,1)+x2(1,1);
    vec1(1,T2:T2+T1-1)=x1(2,:);
    figure (1)
    hFig = figure(1);
    set(hFig, 'Position', [0 0 1000 1000])
    filename = 'testAnimated.gif';
    ttt=1;
    for m=0:T1+T2-2
        vec2(1,1+m:T2+m)=fliplr(x2(2,:));
        x3(2,m+1)=sum(vec1.*vec2);
        subplot(4,1,4)
        stem(x3(1,:),x3(2,:),'r','LineWidth',3)
        axis([Tec2(1),T1+2*T2-2,  min(x3(2,:))-1 max(x3(2,:))+1])
        ylim('auto')
        ylabel('x_3[n]','FontWeight','bold','FontSize',16);
        xlabel('n','FontWeight','bold','FontSize',16);
        grid on
        subplot(4,1,1)
        stem(x2(1,:),x2(2,:),'k','LineWidth',3)
        ylabel('x_2[m]','FontWeight','bold','FontSize',16);
        xlabel('m','FontWeight','bold','FontSize',16);
        title('CONVOLUCIóN','FontWeight','bold','FontSize',16);
        grid on
        axis([Tec2(1),T1+2*T2-2, min(x2(2,:))-1 max(x2(2,:))+1])
        ylim('auto')
        subplot(4,1,2)
        stem(x1(1,:),x1(2,:),'b','LineWidth',3)
        ylabel('x_1[m]','FontWeight','bold','FontSize',16);
        xlabel('m','FontWeight','bold','FontSize',16);
        grid on
        axis([Tec2(1),T1+2*T2-2, min(x1(2,:))-1 max(x1(2,:))+1])
        ylim('auto')
        subplot(4,1,3)
        stem(Tec2,vec2(1,:),'g','LineWidth',3)
        axis([Tec2(1),T1+2*T2-2,min(vec2)-1, max(vec2)+1 ])
        ylim('auto')
        ylabel('x_2[n-m]','FontWeight','bold','FontSize',16);
        xlabel('m','FontWeight','bold','FontSize',16);
        grid on
        drawnow;
        pause(0.4)
        vec2 = zeros(1,T1+2*T2-2);
        frame = getframe(hFig); 
        im = frame2im(frame); 
        [imind,cm] = rgb2ind(im,256); 
        % Write to the GIF File 
        if ttt == 1 
          imwrite(imind,cm,filename,'gif', 'Loopcount',inf); 
        else 
          imwrite(imind,cm,filename,'gif','WriteMode','append'); 
        end
        ttt=ttt+1;
    end
end

Si ejecutamos las siguientes instrucciones en el Command Window y el directorio de trabajo es el mismo donde se encuentra la función convdisc tendrémos el siguiente resultado

n=0:20;
a=[0 1 2 3 4 5 0 0 0 0 0 0 0 0 0 5 4 3 2 1 0];
b=[0 0 0 0 0 5 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0];
convdisc([n;a],[n;b])

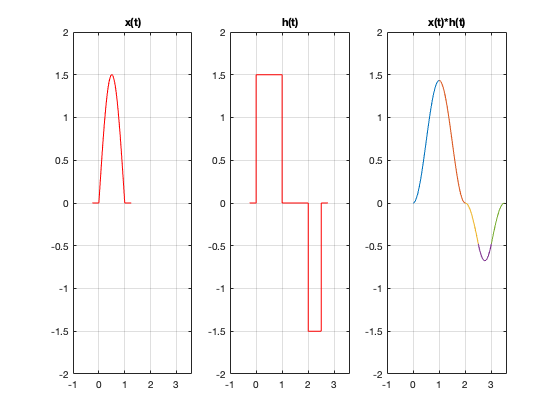
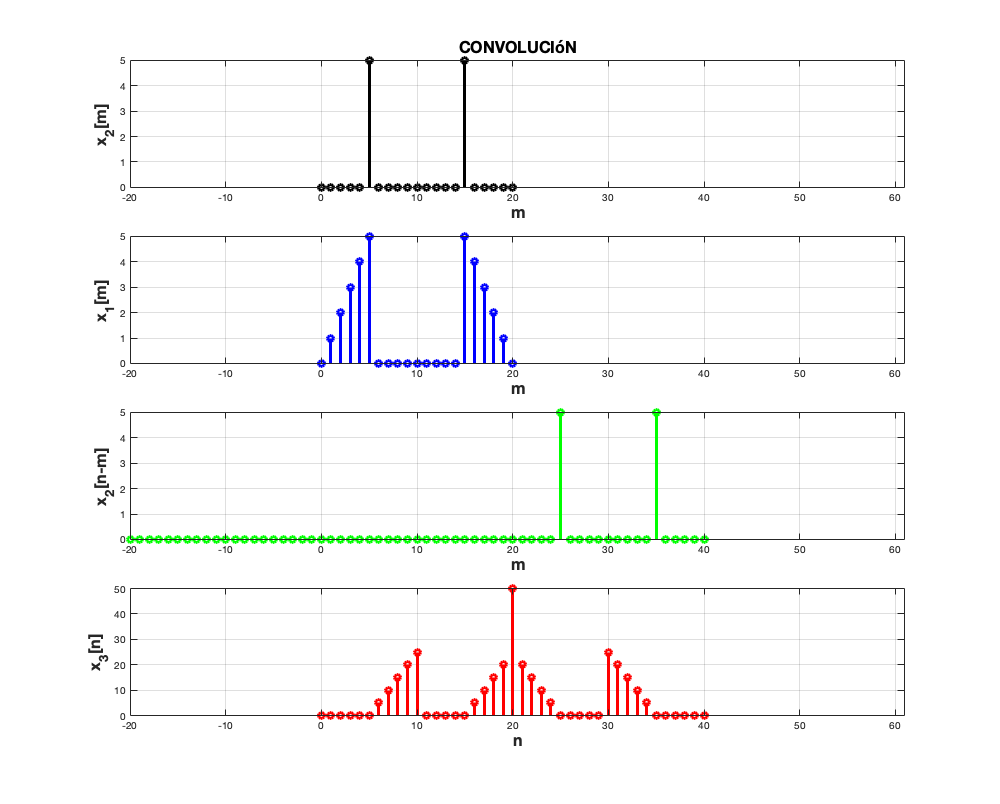
Correlación de señales en tiempo discreto

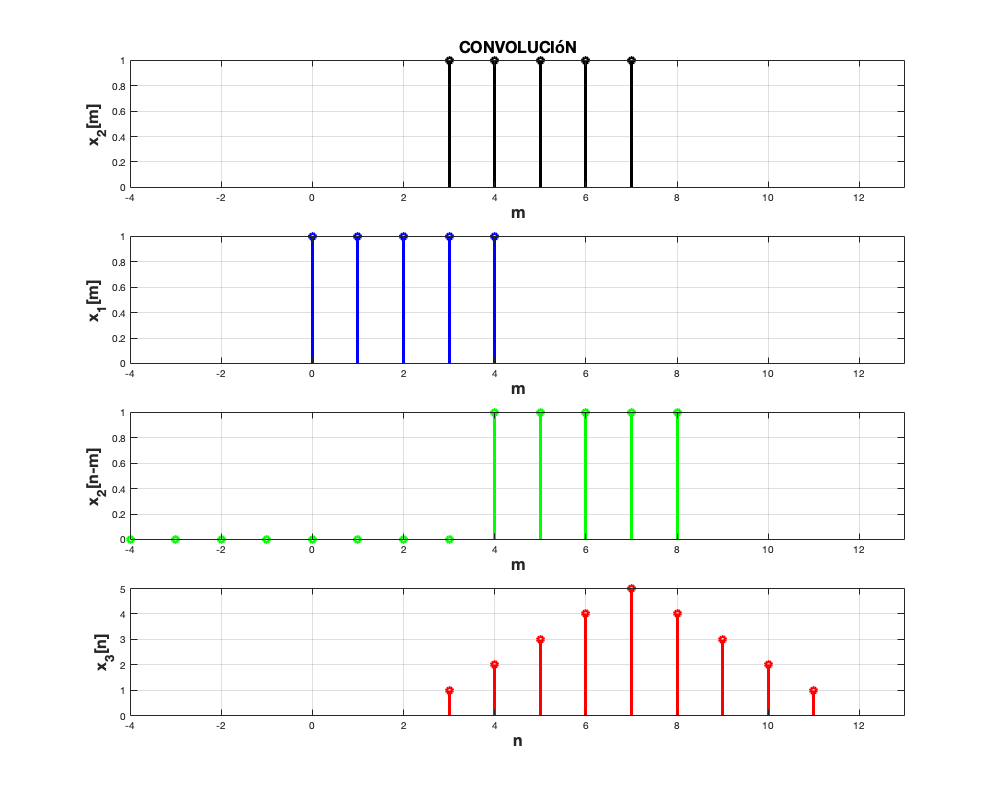
Si se quisiera hacer la correlación de las señales 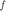$f$ y $g$ recordemos que $r_{fg}[n]=f[n]*g[-n]$ , entonces si

$$f[n]=u[n]-u[n-5]$$

$$g[n]=u[n+7]-u[n+2]$$

Se podría utilizar el código de convolución para resolver este problema

nf=0:4;
f=@(n) n>=0 & n<=4;
ng=3:7;
g=@(n) n>=3 & n<=7;
convdisc( [nf;f(nf)], [ng;g(ng)] )

Entregables

Se revisa una publicación (html) de la práctica. En este caso inicie indicando el nombre de la práctica y sus datos personales, equipos de dos o tres personas (Portada). El índice del contenido lo genera Publish (Índice). Los objetivos son los sigueintes:

Conocer métodos básicos de integración numérica
Manipulación de instrucciones en MATLAB
Simular convoluciones y correlaciones de señales continuas
Simular convoluciones y correlaciones de señales discretas

Como introducción elabore un reporte de los métodos descritos en la lista de reproducción que incluya el desarrollo de los ejemplos expuestos.

Para el desarrollo se tienen que resolver cada uno de los siguientes problemas comenzando una nueva sección (para la publicación) en cada uno de ellos.

Para cada problema se tendrán que hacer las modíficaciones necesarias al código de ejemplo, convendría entonces pensar en realizar una modificación general de tal manera que el programa funcione para cualesquiera dos funciones, pero esto es opcional.

Para el PR04 reporte la grafica de la simulación númerica de la convolución y compare con el resultado análitico que obtuvo para el problema 1, esto es, su práctica tendrá que incluir una llamada a la funciónn convconm y posteriormente se tendrá que mostrar (mediante el Publish) la gráfica tanto de las señales involucradas como el resultado de la convolución, y en esta última gráficara su resultado analitico, se tendrá que incluir el resultado analitico.
Para el PR05 reporte la grafica de la simulación númerica de la correalción y compare con el resultado análitico que obtuvo para el problema e), esto es, su práctica tendrá que incluir una llamada a la funciónn convconm y posteriormente se tendrá que mostrar (mediante el Publish) la gráfica tanto de las señales involucradas como el resultado de su correlación, y en esta última graficara su resultado analitico, se tendrá que incluir el resultado analitico.
Realice la simuación de la convolución de las señales (c) con (d) del problema 3.1.1
Realice la simuación de la correlación de las señales (c) con (d) del problema 3.1.1
Realice la la convolución de las señales (c) con (d) del problema 3.1.1 utilizando el comando conv de MATLAB, muestre el código utilizado y gráfique el resultado, sugerencia: Utilice las propiedades de traslación de la convolución.