Práctica 6: Sistemas diferenciales

Contents

Nota

Se tiene que MATLAB presenta una definición del escalón unitario heaviside(t), donde heaviside(0)=0.5, para versiones mayores o iguales a 2016 esto puede configurarse al valor que se quiera, en nuestro caso queremos heaviside(0)=1, esto se logra ejecutando la siguiente instrucción

sympref('HeavisideAtOrigin', 1);

de no ser posible establecer la configuración se tiene que tener en cuenta la definición de MATLAB.

Sistemas diferenciales (Transformada de Fourier)

Se utiliza el toolbox con herramientas de matemáticas símbolicas, para generar un programa que resuelve sistemas diferenciales de orden n mediante transformada de Fourier, el programa despliega: paso por paso la metodología de solución, la solución de la ecuación diferencial, y la gráfica tanto de la señal de entrada como de la señal de salida. El código programado es el siguiente

function fourier2016a(a,b,xi,t0)
% a coeficientes de las derivadas de la salida menor a mayor [a_0, ..., a_n]
% b coeficientes de las derivadas de la entrada menor a mayor [b_0, ..., b_m]
% xi función de entrada en terminos de la variable simbolica t previamente
% declarada en el command window
% t0 tiempo final para graficar la solucion, la derivada, y la segunda 
% derivada 
% ejemplo: resolver y^(2)+2y^(1)+2y=x^(1)+2x con y^(1)(0)=0
% y(0)=0, x(0)=0, x(t)=exp(-t)u(t), para 5 segundos, se resuleve como
% syms t
% fourier2016a([2 2 1],[2 1],exp(-t)*heaviside(t),5)
close all
tam=size(a);
tami=size(b);
syms y(t) Y(w) x(t) X(w) Yy fp;
syms edd edi 
edd=0;
edi=0;

for i=1:tam(2)
   edd=edd+a(i)*(j*w)^(i-1)*Y(w);
end

for i=1:tami(2)
   edi=edi+b(i)*(j*w)^(i-1)*X(w);  
end
mensaje('APLICAMOS TRANSFORMADA DE FOURIER')

pretty(edd)
disp('=')
pretty(edi)

mensaje('SUBSTITUIMOS LA TRANSFORMADA DE LA ENTRADA')

edi=subs(edi,X(w), fourier(xi));
pretty(edd)
disp('=')
pretty(edi)

mensaje('DESPEJAMOS Y(w)')

edd=collect(edd,Y(w));
edd=subs(edd,Y(w),Yy);
eq1=edd==edi;
disp('Y(w)=')
edd=solve(eq1, Yy);
pretty(edd)

%%% Para versiones superiores a 2016
mensaje('DESARROLLAMOS LAS FRACCIONES PARCIALES DE Y(w)')
disp('Y(w)=')
pretty(partfrac(edd))
%%%% Si se ejecuta en 2015 o menor comentar las 3 lineas anteriores
 
mensaje('Aplicamos transformada inversa, asi la solución es')
disp('y(t)=')
y(t)=ifourier(edd,t);
pretty(y(t))

figure (1)
hFig = figure(1);
set(hFig, 'Position', [0 0 900 900])
axes1 = axes('Parent',hFig,'FontWeight','bold','FontSize',16);
tiempo=0:0.01:t0;
fplot(xi,[0, t0],'b','LineWidth',2)
hold on
fplot(y,[0,t0],'r','LineWidth',2)
legend('Entrada x(t)','Salida y(t)','Location','Best')
xlabel('tiempo','FontWeight','bold','FontSize',16)
title('Entrada y Respuesta del sistema','FontWeight','bold','FontSize',16)
grid on
end

function mensaje(texto)
disp( ' ')
disp(texto)
disp( ' ')
end

Entonces si se quiere resolver la ecuación diferencial

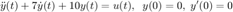
$$\ddot{y}(t)+7\dot{y}(t)+10y(t)=u(t),\;\;y(0)=0,\;y'(0)=0$$

Se ejecutan las siguientes instrucciones, aquí es importante recordar que transformada de Fourier solo resuelve ecuaciones diferenciales donde las condiciones iniciales son nulas.

syms t
fourier2016a([10 7 1],[1],heaviside(t),10)

 
APLICAMOS TRANSFORMADA DE FOURIER
 
           2
10 Y(w) - w  Y(w) + w Y(w) 7i

=
X(w)

 
SUBSTITUIMOS LA TRANSFORMADA DE LA ENTRADA
 
           2
10 Y(w) - w  Y(w) + w Y(w) 7i

=
              1i
pi dirac(w) - --
               w

 
DESPEJAMOS Y(w)
 
Y(w)=
              1i
pi dirac(w) - --
               w
----------------
   2
- w  + w 7i + 10

 
DESARROLLAMOS LAS FRACCIONES PARCIALES DE Y(w)
 
Y(w)=
         w 1i                  7
         ---- - pi dirac(w) + --
   1i     10                  10
- ---- - -----------------------
  10 w          2
             - w  + w 7i + 10

 
Aplicamos transformada inversa, asi la solución es
 
y(t)=
/ pi   pi sign(t)   pi exp(-2 t) (sign(t) + 1)   pi exp(-5 t) (sign(t) + 1)
| -- + ---------- - -------------------------- + --------------------------
\ 10       10                    6                           15

     pi exp(-2 t) dirac(t)   pi exp(-5 t) dirac(t) \
   - --------------------- + --------------------- |/(2 pi)
               15                      15          /

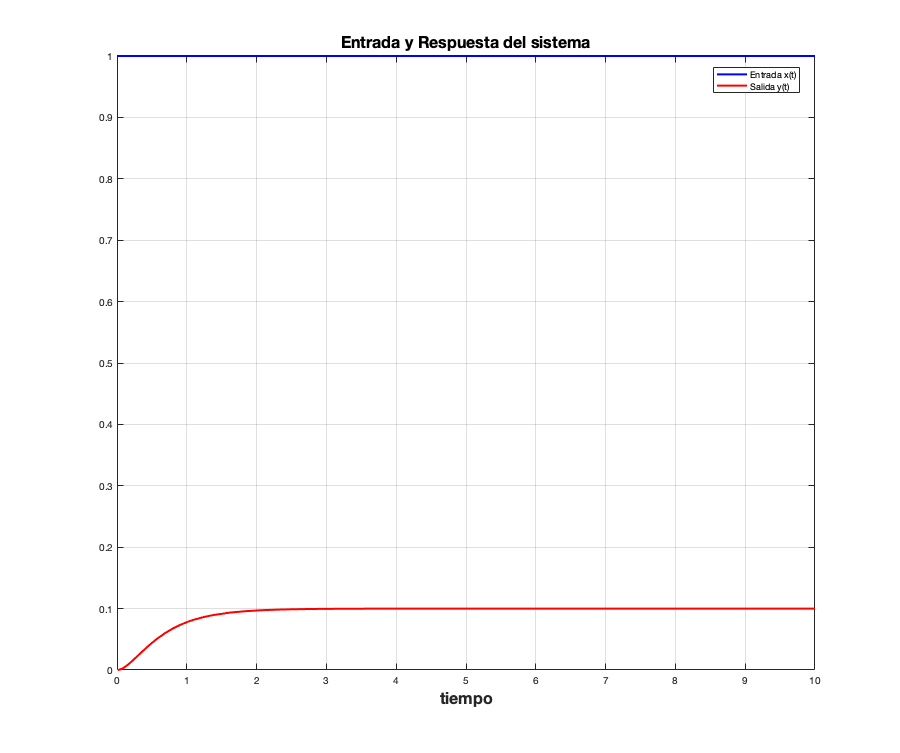
Se observa que la expresión resultante no esta totalmente simplificada, posiblemente con algunas modificaciones de las instrucciones el resultado pueda desplegarse de manera simplificada, también se observa que las fracciones parciales no estan totalmente desarrolladas, la manipulación de símbolos en MATLAB no es lo suficientemente robusta, pero es buena. Ahora observemos el resultado que se ha optenido en el siguiente enlace

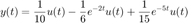
$$y(t)=\frac{1}{10}u(t)-\frac{1}{6}e^{-2t}u(t)+\frac{1}{15}e^{-5t}u(t)$$

En la gráfica se puede observar consistencia, pues observamos que cuando 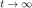$t\to\infty$ el resultado tiende a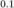 $0.1$

Sistemas diferenciales (Transformada de Laplace)

Se utiliza el toolbox con herramientas de matemáticas símbolicas, para generar un programa que resuelve sistemas diferenciales de orden n mediante transformada de Laplace, y condiciones iniciales en 0 por la izquierda (cero menos) el programa despliega: paso por paso la metodología de solución, la solución de la ecuación diferencial, y la gráfica tanto de la señal de entrada como de la señal de salida y una gráfica de la primera y segunda derivada de la salida. El código programado es el siguiente

function laplace2016a(a,b,ciy,xi,t0)
% a coeficientes de las derivadas de la salida menor a mayor [a_0, ..., a_n]
% b coeficientes de las derivadas de la entrada menor a mayor [b_0, ..., b_m]
% ciy condiciones iniciales de la salida de  menor a mayor [y(0), y(0)^(n-1)]
% xi función de entrada en terminos de la variable simbolica t previamente
% declarada en el command window
% t0 tiempo final para graficar la solucion, la derivada, y la segunda 
% derivada 
% ejemplo: resolver y^(3)+y^(2)+2y^(1)+2y=3x^(2)-x^(1)+2x con y^(2)(0)=1 y^(1)=3
% y(0)=2, x(t)=exp(-t)cos(t)u(t), para 10 segundos, se resuleve como
% syms t
% laplace2016a([2 2 1 1],[2 -1 3],[2 3 1],exp(-t)*cos(t)*heaviside(t),10)
close all
tam=size(a);
tami=size(b);
syms y(t) Y(s) x(t) X(s) Yy fp;
syms edd edi 
edd=0;
edi=0;

for i=1:tam(2)
   edd=edd+a(i)*s^(i-1)*Y(s);
   for k=1:i-1
       edd=edd-a(i)*(s^(i-1-k)*ciy(k));
   end
end

for i=1:tami(2)
   edi=edi+b(i)*s^(i-1)*X(s);
   %for k=1:i-1
     %  edi=edi-b(i)*(s^(i-1-k)*cix(k));
   %end
end
mensaje('APLICAMOS TRANSFORMADA DE LAPLACE y subtituimos condiciones iniciales')

pretty(edd)
disp('=')
pretty(edi)

mensaje('SUBSTITUIMOS LA TRANSFORMADA DE LA ENTRADA')

edi=subs(edi,X(s), laplace(xi));
pretty(edd)
disp('=')
pretty(edi)

mensaje('DESPEJAMOS Y(s)')

edd=collect(edd,Y(s));
edd=subs(edd,Y(s),Yy);
eq1=edd==edi;
disp('Y(s)=')
edd=solve(eq1, Yy);
pretty(simplify(edd))

%%% Para versiones superiores a 2016
mensaje('DESARROLLAMOS LAS FRACCIONES PARCIALES DE Y(s)')
disp('Y(s)=')
pretty(partfrac(edd))
%%%% Si se ejecuta en 2015 o menor comentar las 3 lineas anteriores

mensaje('Aplicamos transformada inversa, asi la solución es')
disp('y(t)=')
y(t)=ilaplace(edd);
pretty(y(t))

dy(t)=diff(y,t);
ddy(t)=diff(dy,t);
figure (1)
hFig = figure(1);
set(hFig, 'Position', [0 0 900 900])
axes1 = axes('Parent',hFig,'FontWeight','bold','FontSize',16);
tiempo=0:0.01:t0;
subplot(2,1,1)
fplot(xi,[0, t0],'b','LineWidth',2)

hold on
fplot(y,[0,t0],'r','LineWidth',2)

legend('Entrada x(t)','Salida y(t)','Location','Best')
xlabel('tiempo','FontWeight','bold','FontSize',16)
title('Entrada y Respuesta del sistema','FontWeight','bold','FontSize',16)
grid on
subplot(2,1,2)
fplot(dy,[0,t0],'g','LineWidth',2)

hold on
title('Primera y segunda derivada de la salida','FontWeight','bold','FontSize',16)
fplot(ddy,[0,t0],'m','LineWidth',2)

legend('dy(t)/dt','d^2y(t)/d^2t','Location','Best')
xlabel('tiempo','FontWeight','bold','FontSize',16)
grid on
end

function mensaje(texto)
disp( ' ')
disp(texto)
disp( ' ')
end

Entonces si se quiere resolver la ecuación diferencial

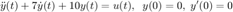
$$\ddot{y}(t)+7\dot{y}(t)+10y(t)=u(t),\;\;y(0)=0,\;y'(0)=0$$

Se ejecutan las siguientes instrucciones,

syms t
laplace2016a([10 7 1],[1],[0,0],heaviside(t),10)

 
APLICAMOS TRANSFORMADA DE LAPLACE y subtituimos condiciones iniciales
 
                      2
10 Y(s) + 7 s Y(s) + s  Y(s)

=
X(s)

 
SUBSTITUIMOS LA TRANSFORMADA DE LA ENTRADA
 
                      2
10 Y(s) + 7 s Y(s) + s  Y(s)

=
1
-
s

 
DESPEJAMOS Y(s)
 
Y(s)=
        1
-----------------
    2
s (s  + 7 s + 10)

 
DESARROLLAMOS LAS FRACCIONES PARCIALES DE Y(s)
 
Y(s)=
     1           1         1
---------- - --------- + ----
15 (s + 5)   6 (s + 2)   10 s

 
Aplicamos transformada inversa, asi la solución es
 
y(t)=
exp(-5 t)   exp(-2 t)    1
--------- - --------- + --
    15          6       10

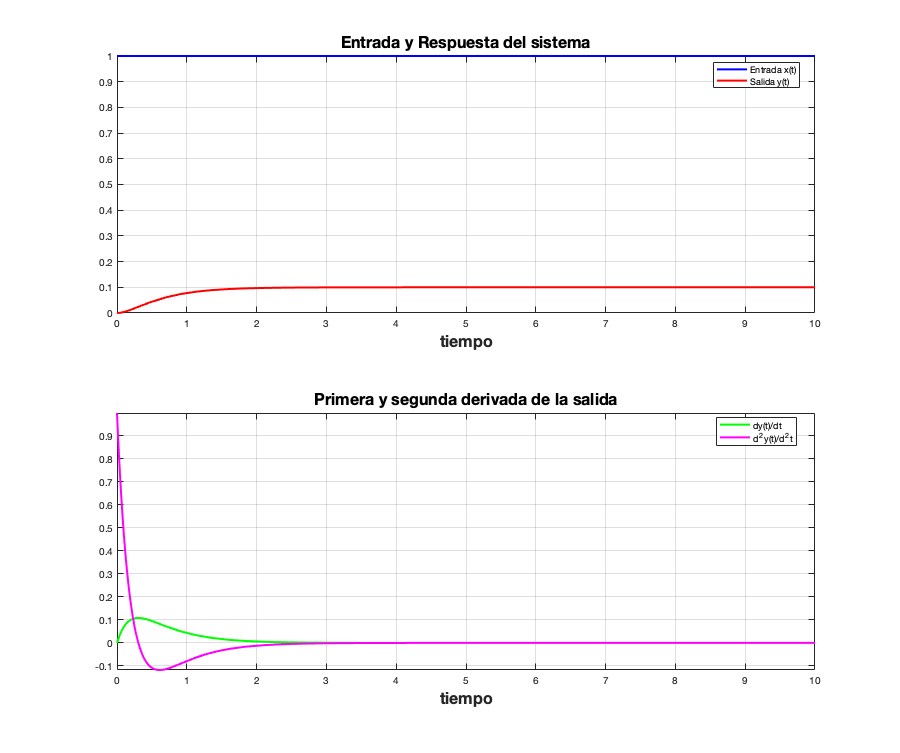
Se observa que la expresión resultante esta totalmente simplificada, posiblemente por que es este caso no hay manipulaciópn de deltas de Dirac, es general la manipulación de símbolos en MATLAB no es lo suficientemente robusta, pero es buena. Ahora observemos el resultado que se ha optenido en el siguiente enlace

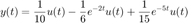
$$y(t)=\frac{1}{10}u(t)-\frac{1}{6}e^{-2t}u(t)+\frac{1}{15}e^{-5t}u(t)$$

Así se lográ observar que el resultado es identico

Entregables

Para sistemas diferenciales realiza un programa con las siguientes características

  1. Muestra la función de transferencia del sistema
  2. Muestra la respuesta al impulso (simbólico, gráfica)
  3. Muestra la respuesta a entrada cero (simbólico, gráfica)
  4. Muestra la respuesta a estado cero (simbólico, gráfica)
  5. Muestra la respuesta total (simbólico, gráfica)
  6. La respuesta total al escalón con condiciones iniciales 0 (simbólico, gráfica)
  7. Usando subplot, depliega una figura con 5 gráficas

Observa que los entregables pueden resolverse (solvo la función de transferencia) con llamadas a la funciones presentadas en esta publicación

Nota: Ejecuta los ejemplos descritos dentro de los comentarios de cada código para que observes el uso de estos

Se entrega una publicación en html de tu desarrollo y se probará para un problema específico.

El código de esta publicación lo puedes encontrar en el siguiente enlace


Published with MATLAB® R2019a