Contents

Un tipo de ecuaciones en diferencias

La forma general de una ecuación en diferencias de primer orden es:

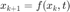
$$x_{k+1}=f(x_k,t)$$

Si no hay dependencia explicita de t en la función 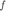$f$ decimos que la ecuación es autonoma.

No pretendemos agotar este tema, nuestro objetivo es dar algunos elementos para el reporte que se esta trabajando.

Se puden consultar los dos primeros videos de la siguiente lista para ver ejemplos:

Para continuar, a este punto se debe de tener claro que es un punto de equilibrio, (punto fijo, punto estacionario, etc ) y la estabilidad del punto de equilibrio. Sino se tiene claro, consulta otras referencias.

Se puede pensar en la necesidad de resolver ecuaciones en diferencia simultaneas autonomas (acotamos nuestro estudio a dos ecuaciones). Si estas son lineales y de coeficientes constantes, existen herramientas matemáticas para atacar y resolver este problema. Tanto de forma análitica como de forma númerica.

Consideremos el siguente sistema de ecuaciones en diferencia

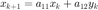
$$x_{k+1}=a_{11}x_k+a_{12}y_k$$

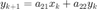
$$y_{k+1}=a_{21}x_k+a_{22}y_k$$

con condiciones iniciales $x_0$ y $y_0$

Ejemplo 1:

Encontrar las primeras 20 iteraciones del sistema

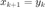
$$x_{k+1}=y_k$$

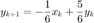
$$y_{k+1}=-\frac{1}{6}x_k+\frac{5}{6}y_k$$

con condiciones iniciales

$x_0=100$ y $y_0=-500$

[x,y] = sistema(0,1,-1/6,5/6,100,-500,20);

Gráficamos las simulaciones por separado

n = 0:20;
figure
stem(n,x)
figure
stem(n,y)

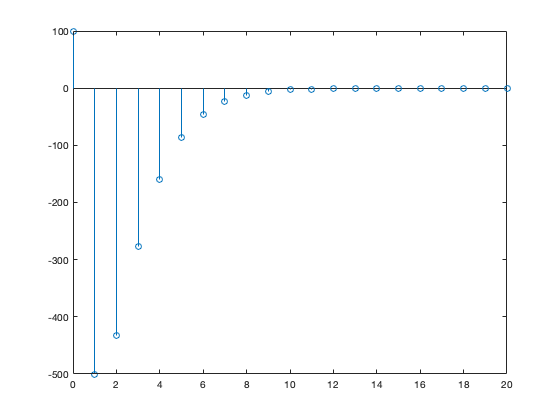
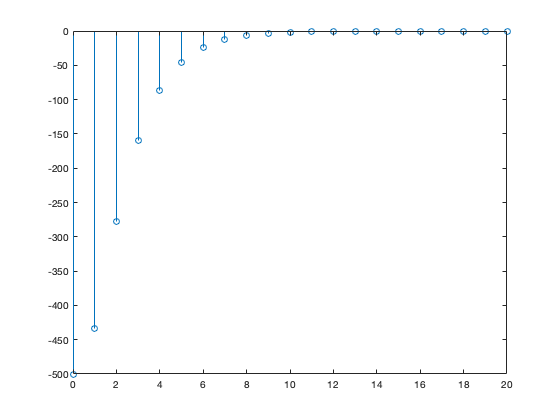
Al observar las trayectorias de las dos variables se intuye que el punto de equilibrio (en este caso el 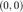$(0,0)$) es estable.

Realizamos una grafica de los valore de 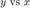$y\mbox{ vs } x$ (a esto se le llama plano fase). En el plano fase observamos la trayectoria del sistema de forma conjunta, esta converge al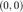 $(0,0)$

n = 0:20;
figure
plot(x,y,'o')
hold on
plot(x,y)

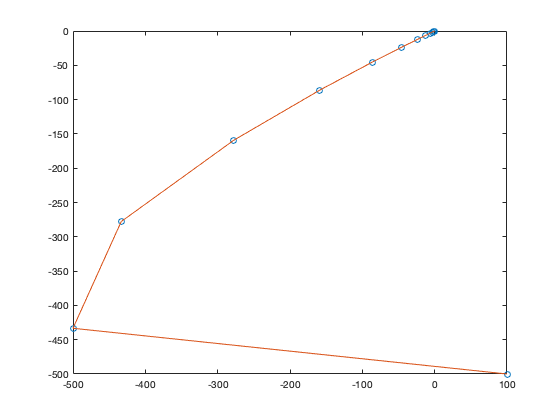
Podemos escribir el sistema de ecuaciones dentro de una matriz

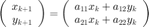
$$\left(\begin{array}{c}x_{k+1}\\y_{k+1}\end{array}\right)=\left(\begin{array}{c}a_{11}x_k+a_{12}y_k\\a_{21}x_k+a_{22}y_k\end{array}\right)$$

condiciones iniciales 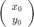$$\left(\begin{array}{c}x_0\\y_0\end{array}\right)$$

El significado es el mismo (definición de igualdad de matrices entrada por entrada)

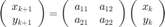
$$\left(\begin{array}{c}x_{k+1}\\y_{k+1}\end{array}\right)=\left(\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\right)\left(\begin{array}{c}x_k\\y_k\end{array}\right)$$

con condiciones iniciales

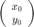
$$\left(\begin{array}{c}x_0\\y_0\end{array}\right)$$

algunas veces convendra escribir

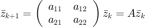
$$\bar{z}_{k+1}=\left(\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\right)\bar{z}_k=A\bar{z}_k$$

con condición inicial $\bar{z}_0$

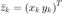Donde $\bar{z}_k = \left(x_k\,y_k\right)^T$, solo en una definición de notación.

En particular nos interesa ver la relación entre los valores propios de la matriz del sistema (el sistema de ecuaciones en forma matricial) y el comportamiento que este tiene en cuestion de convergencia.

Si resolvemos el Ejemplo 1 en forma matricial

Ejemplo 2:

Encontrar las primeras 20 iteraciones del sistema

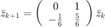
$$\bar{z}_{k+1}=\left(\begin{array}{cc}0&1\\-\frac{1}{6}&\frac{5}{6}\end{array}\right)\bar{z}_k$$

condición inicial 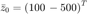$\bar{z}_0=\left(100\,-500\right)^T$

A=[0 1;
  -1/6 5/6];

z0 =[100 -500]';

z = sistemaM(A,z0,20);

Gráficamos el plano fase

n = 0:20;
figure
plot(z(1,:),z(2,:),'o')
hold on
plot(z(1,:),z(2,:))

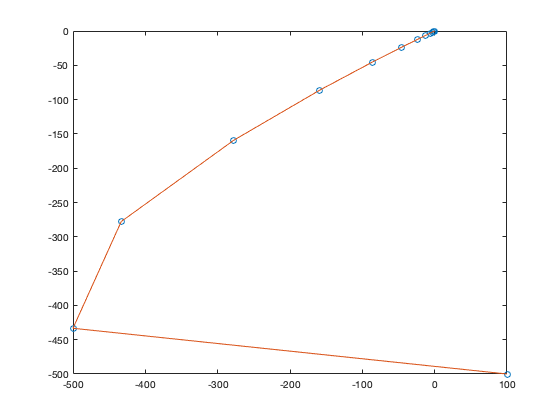
Igual a lo obtenido en forma escalar.

Ahora obsevemos los valores propios de A

eig(A)

ans =

    0.3333
    0.5000

Se puede caracterizar la estabilidad del sistema de acuerdo a los valores propios. Precisamos la ubicación y el tipo de comportamiento en la sigueinte sección

Estabilidad en el sentido de Lyapunov

Este tipo de estabilidad (existen varias definiciones) esta asociada a la respuesta a entrada cero (del sistema), la definición caracteriza el comportamiento del sistema en el siguiente sentido.

La respuesta a entrada cero de un sistema LTI en diferencias, es marginalmente estable o estable en el sentido de Lyapunov si cada condición inicial finita genera una respuesta acotada. Si adicionalmente la respuesta tiende a cero cuando el tiempo tiende a infinito diremos que la respuesta es asintoticamente estable. Cuando esto no suceda (no acotada, no tiende a cero) diremos que la respuesta asociada es inestable.

Esta definición se puede verificar con las siguientes condiciones

En el caso del ejemplo 2 (ejemplo 1 en forma matricial) tenemos un punto de equilibrio asintoticamente estable (valores propios con norma menor a la unidad).

Hay algunas cuestiones técnicas de vocabulario que no se quieren precisar para no perder el objetivo, pero todo lo que se esta diciendo tiene sentido (hablar de la estabilidad del sistema o de la estabilidad de la solución de equilibrio coincide en sistemas LTI).

Ahora revisemos dos ejemplos más, directamente establecemos la matriz del sistema y las condiciones iniciales:

Ejemplo 3

A=[-0.5 0.5;
   0.5 0.5]

z0 =[100 -500]';

z = sistemaM(A,z0,20);

A =

   -0.5000    0.5000
    0.5000    0.5000


n = 0:20;
figure
plot(z(1,:),z(2,:),'o')
hold on
plot(z(1,:),z(2,:))

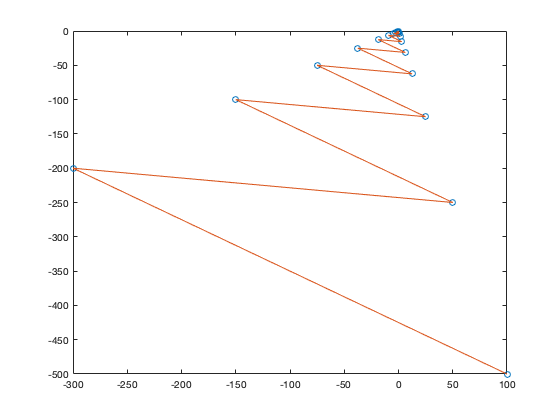
eig(A)
trace(A)
det(A)
%

ans =

   -0.7071
    0.7071


ans =

     0


ans =

   -0.5000

Ejemplo 4

A=[-1 -1.5;
   1 1]

z0 =[100 -500]';

z = sistemaM(A,z0,20);

A =

   -1.0000   -1.5000
    1.0000    1.0000


n = 0:20;
figure
plot(z(1,:),z(2,:),'o')
hold on
plot(z(1,:),z(2,:))

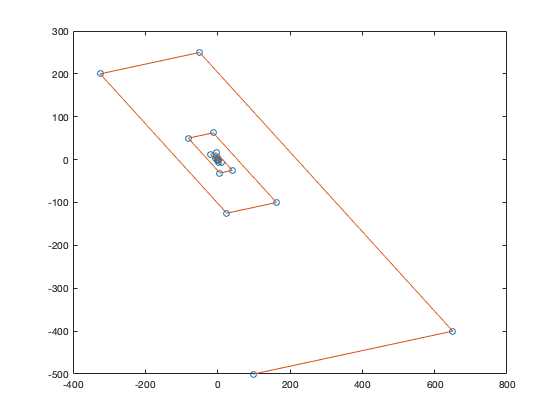
eig(A)
trace(A)
det(A)

ans =

   0.0000 + 0.7071i
   0.0000 - 0.7071i


ans =

     0


ans =

    0.5000

Observemos que en el ejemplo 3 y en el ejemplo 4, ambos sistemas son asintoticamente estables (valores propios con norma menor a uno). Pero la "forma" en la que convergen al punto de equilibrio 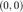$(0,0)$ es diferente, esto como conclusión de observar su plano fase.

También observamos que los valores de traza y determinante de cada matriz son distintos.

Resulta que se puede hablar de la "forma de convergencia" (tipo de punto equilibrio) de acuerdo a un analisis más detallado de los valores propios, pero tambien resulta que los valores propios de una matriz $A$ (de 2 por 2) se pueden escribir en términos de su traza y determinante.

Así, es posible hacer una gráfica donde a partir de los valores de la traza y determinante de una matriz $A$ se pueda caracterizar el comportamiento del punto de equilibrio (un poco más alla de decir el tipo de estabilidad).

En esta dirección, en el ejemplo 3 decimos que el punto de equilibrio es un nodo estable. Para el ejemplo 4 decimos que el punto de equilibrio es una espiral estable. Y en terminos de su valor de traza y determinante, se encuentran en la región III y región IV de la siguiente figura respectivamente:

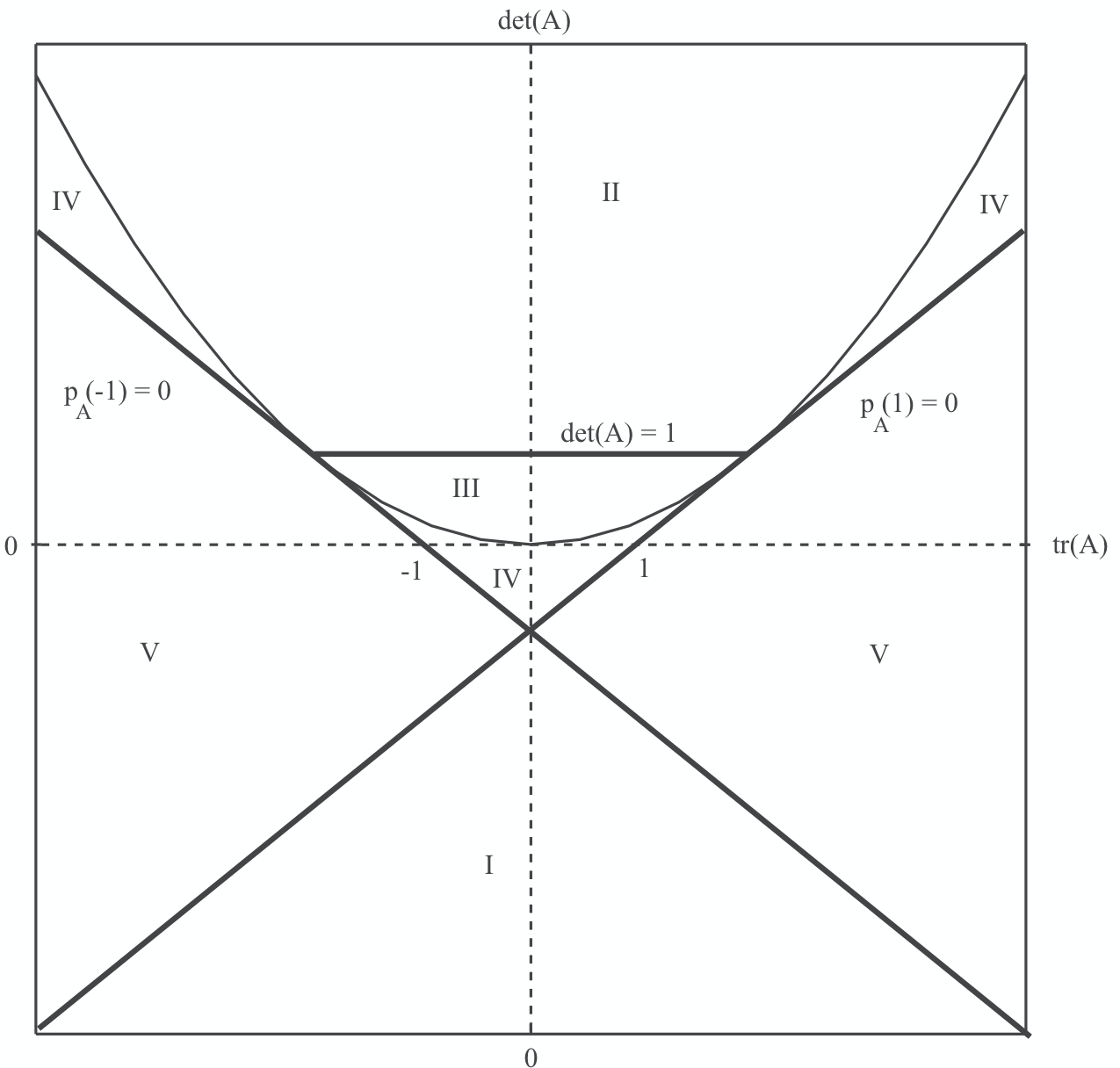
donde 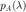$p_A(\lambda)$ es el polínomio caracteristico de la matriz $A$

Códigos

function [x,y] = sistema(a11,a12,a21,a22,x0,y0,n)
x(1) = x0;
y(1) = y0;
for i=2:n+1
    x(i) = a11*x(i-1) + a12*y(i-1);
    y(i) = a21*x(i-1) + a22*y(i-1);
end

end


function z = sistemaM(A,z0,n)
z = z0;
for i=2:n+1
    zk = A*z0;
    z = [z zk];
    z0 = zk;
end

end


Published with MATLAB® R2021a