Práctica 5: Series de Fourier en tiempo continuo

Contents

Programa serie de Fourier exponencial compleja

La serie de Fourier de una señal 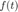periódica puede ser construida bajo ciertas condiciones matemáticas (las condiciones de Dirichlet, aunque estas podrían no cumplirse y aún así la serie existir) de la señal. Si la señal no es periódica pero cumple las condiciones en un intervalo de longitud finita, se puede construir la serie de Fourier en el intervalo (cuando el intervalo es de longitud infinita se puede abordar a la suma de Fourier, exponencial compleja, como una integral y los coeficientes 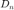son muestras de lo que llamamos transformada de Fourier.)

Deberás realizar algunos problemas con las especificaciones que se encuentran al final del documento, para ello se proporciona el siguiente código, que gráfica la serie de Fourier exponencial compleja.

function sfc(t0,tf,dn,d0,f,armo,a,b)
% t0 el valor inicial para calcular la serie
% tf el valor final donde calcular la serie
% dn función de la fórmula de los dn
% f función original
% armo número de armonicos a utilizar en la gráfica
% a, b intevalo para realizar la grafica de la serie

w0=2*pi/(tf-t0);

sf=d0;
t=a:0.0001:b;

for n=1:armo
    sf=sf+dn(-n)*exp(w0*-n*t*j)+dn(n)*exp(w0*n*t*j);
end
figure (1)
hFig = figure(1);
set(hFig, 'Position', [0 0 900 900])
subplot(3,2,1)
plot(t,sf,'LineWidth',2)
grid on
legend('Serie de Fourier','Location','Best')
xlabel('t','FontWeight','bold','FontSize',16)

sf=d0;
t1=t0:0.0001:tf;

for n=1:armo
    sf=sf+dn(-n)*exp(w0*-n*t1*j)+dn(n)*exp(w0*n*t1*j);
end

subplot(3,2,2)
plot(t1,f(t1),'r','LineWidth',2)
grid on
hold on
plot(t1,sf,'LineWidth',2)
legend('Función original','Serie de Fourier ','Location','Best')
xlabel('t','FontWeight','bold','FontSize',16)
nn=-armo:armo;
axis auto

subplot(3,2,4)
e=f(t1)-sf;
plot(t1,e,'LineWidth',2)
title('Error','FontWeight','bold','FontSize',16)
xlabel('t','FontWeight','bold','FontSize',16)
axis auto
grid on

subplot(3,2,6)
e=f(t1)-sf;
area(t1,e.^2)
legend('Energia del error','Location','Best')
xlabel('t','FontWeight','bold','FontSize',16)
axis auto
grid on

absdn=zeros(1,length(nn));
cont=1;
for i =-armo:armo
    if i==0
        absdn(cont)=d0;
    end
    
    absdn(cont)=dn(i);
    cont=cont+1;
end

subplot(3,2,3)
stem(w0*nn,abs(absdn),'LineWidth',2)
title('Espectro de magnitud D_n ','FontWeight','bold','FontSize',16)
xlabel('\omega','FontWeight','bold','FontSize',16)
grid on

subplot(3,2,5) % % 
stem(w0*nn,angle(absdn),'LineWidth',2) % % 
title('Espectro de fase, \angle de D_n ','FontWeight','bold','FontSize',16) % % 
xlabel('\omega','FontWeight','bold','FontSize',16)
grid on

end

Por ejemplo si

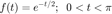
periódica, entonces si se calcula la serie de Fourier exponencial compleja se utilizan las siguientes instrucciones para observar las gráficas correspondientes

d0=0.504;
dn=@(n) 0.504/(1+4*n*j);
t0=0;
tf=pi;
f=@(t) exp(-t/2);
armo=4;
a=-7;
b=7;
sfc(t0,tf,dn,d0,f,armo,a,b)

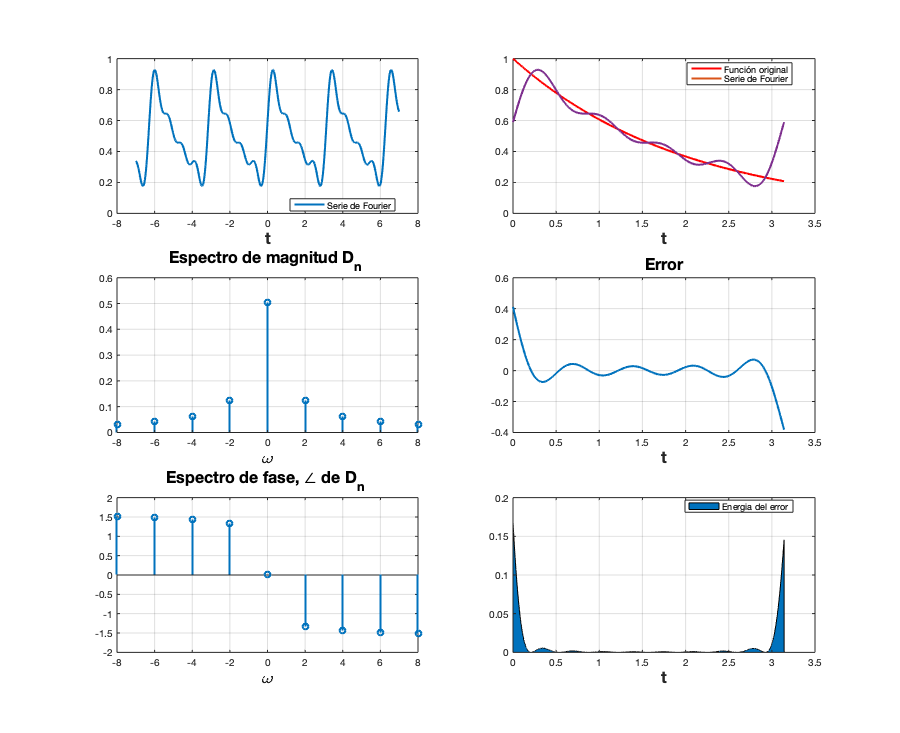
Entregables

Se revisa una publicación (html) de la práctica. En este caso inicie indicando el nombre de la práctica y los datos del equipo (Portada). El índice del contenido lo genera Publish (Índice). Los objetivos son los sigueintes:

No hay investigación para la introducción

Para el desarrollo se tienen que resolver cada uno de los siguientes problemas comenzando una nueva sección (para la publicación) en cada uno de ellos.

Cada problema se realiza para serie trigonométrica compacta y exponencial compleja, cada figura debe contener

No es necesario incluir conclusiones en esta práctica, como apéndices agregue los códigos que utilizó, no olvide incluir sus referencias.

El código de esta publicación lo puedes encontrar en el siguiente enlace

Published with MATLAB® R2019b