Determinantes del crecimiento económico de México: Un enfoque de cointegración

library(dplyr)
library(ggplot2)
library(highcharter)
library(tidyverse)
library(lubridate)
library(openxlsx)
library(DT)
library(data.table)
library(xts)
library(zoo)
library(urca)
library(tseries)
library(xts)
library(forecast)
library(astsa)
library(vars)
library(stargazer)
library(tsDyn)

data <- read.xlsx("Datos/v2005v2.xlsx",
                  detectDates = TRUE)


pib_xts<-xts(data$logpib,
                 order.by = data$FECHA)

cfa_xts<-xts(data$logcaprea,
                 order.by = data$FECHA)

pea_xts<-xts(data$logpea,
                 order.by = data$FECHA)

gp_xts<-xts(data$loggastpub,
                 order.by = data$FECHA)

imp_xts<-xts(data$logimp,
                 order.by = data$FECHA)

exp_xts<-xts(data$logexp,
                 order.by = data$FECHA)

data_xts <- data.frame(pib = pib_xts, cfa = cfa_xts, pea = pea_xts,
                       gp = gp_xts, imp = imp_xts, exp = exp_xts)
#pib_xts
#cfa_xts
#pea_xts
#gp_xts
#imp_xts
#exp_xts

Introducción

En la literatura empírica existe un debate des hace varias decadas sobre la dirección en la relación causal entre la abertura hacía el comercio internacional de un país y su crecimiento económico. Algunos académicos sostienen que los tratados comerciales internacionales favorecen e impulsan el crecimiento de la economía [2]. Estos modelos se definen como de crecimiento impulsado por las exportaciones (CIE) y se fundamentan en las externalidades positivas resultantes de una mejor asignación de los recursos, la posibilidad de economías de escalas y un incremento del crecimiento tecnológico debido a un contexto más competitivo [4]. Otros estudios, al contrario, consideran que son las exportaciones las que determinan el crecimiento económico, y los modelos se definen como de exportaciones impulsadas por el crecimiento (EIC). En este caso un aumento en la productividad local por mejorías tecnológicas o en el capital humano impulsaría las exportaciones y por ende el crecimiento [5]. Finalmente una tercera hipótesis avanzada por la academia es que el crecimiento tenga como determinante principal el aumento de las importaciones(CII). Según esta teoría el crecimiento endógeno se ve favorecido por la posibilidad para las empresas locales de acceder a productos semiacabados y tecnologías extranjeras mejorando su competitividad internacional [7]. En México a partir de los años 80 la política de apertura frente al resto del mundo, promovida por la presidencia de Miguel de la Madrid Hurtado, determina un cambio sustancial con respecto al precedente modelo de sustitución de las importaciones y marca el camino en la definición de la política macroeconómica mexicana siempre más votada hacía un modelo abierto, con la firma del GATT (1986), el NAFTA (1996) y recientemente con la ratificación del T-MEC. A partir de este ex cursus histórico nos preguntamos si efectivamente esta abertura favoreció el crecimiento de la economía mexicana.

Otro factor relevante, cuando consideramos los modelos de crecimiento, es el papel del gasto público como motor del desarrollo económico. Siempre a partir de los años 80, frente a la década perdida, se modificó también la función del estado con respecto a la economía, pasando de un modelo donde este controlaba los sectores económicos estratégicos a uno neoliberal, predominado por la economía de mercado. Justificado por las ineficiencias y fallas de las gestiones de los gobiernos anteriores, la reducción de las funciones del estado fue acompañada por la implementación de severas políticas de estabilización macroeconómica que llevó a un masivo recorte del gasto público en infraestructura económica y social, además de la venta de la mayoría de las empresas paraestatales. Hoy en día, la inversión estatal se encuentra de nuevo al centro de la discusión pública por la política de austeridad promovida por el gobierno de Andrés Manuel López Obrador. En este trabajo se intentará comprender la relación entre esta y el crecimiento económico, mientras por algunos economistas este puede tener un efecto positivo en la economía [9] por otros el impacto a largo plazo es negativo [1].

Modelo teórico y datos

Para intentar entender los efectos de la balanza comercial (importaciones/exportaciones) y del gasto público en crecimiento del Producto Interno Bruto, se incorporaron estos elementos a la función de producción agregada, propuesto entre otros, por Sheehey [10]. La función aumentada de producción por lo tanto tendrá la siguiente especificación:

\[ Y=F[(K,L);GP,X,M]\]

Donde \(Y\) representa el PIB, \(K\) el capital neto real, \(GP\) el gasto público, \(X\) las exportaciones reales y \(M\) las importaciones reales. En la estructuración más sencilla el modelo se asumió como lineal y aditivo.

Respecto a los datos utilizados, se construyeron unas series de tiempo con frecuencia trimestral a partir del \(1-2005\) hasta él \(4-2020\) para capturar las relaciones contemporáneas entre las distintas variables. Los datos fueron desestacionalizados y transformados logarítmicamente para mitigar efectos de escala. Para las estimaciones se utilizaron datos de INEGI. En particular se utilizaron los siguientes indicadores:

• \(Y:\) Producto interno bruto (PIB y cuentas nacionales)
• \(K:\) Formación capital fijo real ajustado (Sistemas de cuentas nacionales)
• \(L:\) Población económicamente activa (ENOE/ETOE)
• \(GP:\) Consumo de gobierno (Oferta y Demanda Global Trimestral)
• \(X:\) Exportación de bienes y servicios (Oferta y demanda global de bienes y servicios)
• \(M:\) Importación de bienes y servicios (Oferta y demanda global de bienes y servicios)

Una vez descritas las variables de interés, en la próxima sección analizaremos el modelo empírico utilizado, al fin de encontrar las relaciones a corto y largo plazo entre estas.

Metodología de estimación

El primer modelo naif que se utilizó para intentar estimar la relación entre las variables de interés fue uno de mínimos cuadrados ordinarios con errores robustos, donde la forma funcional adoptada fue de tipo lineal y aditiva como especificado en la ecuación \(1\):

\[ Y= \beta_0 + \beta_1 K + \beta_2 L + \beta_3 GP + \beta_4 X + \beta_5 M + \epsilon \;\;\;(1) \]

m<- lm(logpib~logcaprea + logpea + loggastpub + logimp + logexp,
        data= data)

stargazer(m, type = "text")

## 
## ===============================================
##                         Dependent variable:    
##                     ---------------------------
##                               logpib           
## -----------------------------------------------
## logcaprea                    0.359***          
##                               (0.073)          
##                                                
## logpea                        0.138**          
##                               (0.055)          
##                                                
## loggastpub                   -0.288***         
##                               (0.073)          
##                                                
## logimp                       0.213***          
##                               (0.047)          
##                                                
## logexp                       0.204***          
##                               (0.046)          
##                                                
## Constant                     2.462***          
##                               (0.217)          
##                                                
## -----------------------------------------------
## Observations                    64             
## R2                             0.993           
## Adjusted R2                    0.992           
## Residual Std. Error       0.004 (df = 58)      
## F Statistic          1,559.644*** (df = 5; 58) 
## ===============================================
## Note:               *p<0.1; **p<0.05; ***p<0.01

El análisis gráfico de los indicadores parece mostrar un elemento de tendencia que invalida el uso de OLS para la estimación de los parámetros y que llevaría a la identificación de relaciones espurias siendo que los supuestos de Markov no se cumplirían.

Logaritmo de las series

myMenuItems <- c("downloadPNG", "downloadJPEG", "downloadPDF", "downloadCSV" )

 highchart(type = "stock")%>% 
  hc_add_series(name= "PIB",
                pib_xts)%>%
  hc_add_series(
    cfa_xts,
    name = "Capital  fijo"
  )%>%
hc_add_series(
    pea_xts,
    name = "Pop. Eco. Act."
  )%>%
   hc_add_series(
    gp_xts,
    name = "Gasto público"
  )%>%
   hc_add_series(
    imp_xts,
    name = "Importaciones"
  )%>%
   hc_add_series(
    exp_xts,
    name = "Exportaciones"
  )%>%
hc_add_theme(hc_theme_economist())%>%
  hc_title(text = "Series en logaritmos")%>%
           #margin = 20, align = "left",
           #style = list(color = "#90ed7d", useHTML = TRUE)) %>% 
  hc_subtitle(text = "2005-2020")%>%
             # align = "left",
            #  style = list(color = "#2b908f", fontWeight = "bold")) %>% 
  hc_yAxis(title = list(text = "log"))%>%
  hc_xAxis(title = list(text = "Fecha (colocar el apuntador sobre
                        las gráficas)"))%>%
  hc_legend(align = "right", verticalAlign = "top",
            layout = "vertical") %>%
    hc_tooltip(valueDecimals=4) %>% 
  hc_exporting(enabled = TRUE,
               filename = "datos",
               buttons = list(contextButton = list(menuItems = myMenuItems)))

A partir de esta constatación y dada la naturaleza de largo plazo entre estas variables se procedió a un test de cointegración para intentar entender la relación de largo plazo entre estas.

Antes de proceder en este análisis se averiguó el orden de integración de cada serie para asegurar que tuvieran el mismo orden y que ese fuera estrictamente mayor que 0. Para hacer eso se utilizaron distintos test de raíz unitaria como el de Dickey-Fuller Aumentado, que realiza un test estadístico t en el parámetro \(\Phi\) de la ecuación \(2\) bajo la hipótesis nula que el parámetro sea igual a \(0\), el KPSS [6] y el ADF-GLS, una variante del ADF donde el parámetro \(\mu_t\) relativo a la parte determinística de la ecuación. Los parámetros en este último caso vienen estimados por medio de un método generalizado de momentos en la primera etapa, y en la segunda etapa una regresión ADF viene efectuada utilizando los residuales de la primera etapa [3]. Esto permite un mayor poder estadístico y una estimación más eficiente. La extensión utilizada en este trabajo fue la de Perron [8]

\[ \Delta y_{t}=\mu_{t}+\varphi y_{t-1}+\sum_{i=1}^{p} y_{i} \Delta y_{t-i}+\epsilon_{t}\;\;(2) \]

Diferencia del logaritmo de las series

myMenuItems <- c("downloadPNG", "downloadJPEG", "downloadPDF", "downloadCSV" )

 highchart(type = "stock")%>% 
  hc_add_series(name= "PIB",
                diff(pib_xts))%>%
  hc_add_series(
    diff(cfa_xts),
    name = "Capital  fijo"
  )%>%
hc_add_series(
    diff(pea_xts),
    name = "Pop. Eco. Act."
  )%>%
   hc_add_series(
    diff(gp_xts),
    name = "Gasto público"
  )%>%
   hc_add_series(
    diff(imp_xts),
    name = "Importaciones"
  )%>%
   hc_add_series(
    diff(exp_xts),
    name = "Exportaciones"
  )%>%
hc_add_theme(hc_theme_economist())%>%
  hc_title(text = "Diferencia series en logaritmos")%>%
           #margin = 20, align = "left",
           #style = list(color = "#90ed7d", useHTML = TRUE)) %>% 
  hc_subtitle(text = "2005-2020")%>%
             # align = "left",
            #  style = list(color = "#2b908f", fontWeight = "bold")) %>% 
  hc_yAxis(title = list(text = "log"))%>%
  hc_xAxis(title = list(text = "Fecha (colocar el apuntador sobre
                        las gráficas)"))%>%
  hc_legend(align = "right", verticalAlign = "top",
            layout = "vertical") %>%
   hc_tooltip( valueDecimals=4) %>% 
  hc_exporting(enabled = TRUE,
               filename = "datos",
               buttons = list(contextButton = list(menuItems = myMenuItems)))

Una vez realizados estos test se definió el orden “optimo” de lags a considerar por medio de unos criterios de información, entre los cuales el BIC, el AIC y el de Hannan-Quinn (HQC), especificado en la ecuación \(3\), que se utilizó como referencia.

\[ HQC = n log (\frac{RSS}{N}) + 2k log n\;\;\;(3) \]

Una vez identificados los lags a incluir en el modelo se realizó un test de Jhoansen para definir el número de vectores cointegrantes. Una vez definido el rango de cointegración por medio del \(\lambda-max\), se procedió a la estimación de un modelo VECM.

Existía una vieja dicotomía entre (a) modelos estructurales que representaban fielmente la teoría macroeconómica pero no se ajustaban a los datos, y (b) modelos de series de tiempo que se adaptaban con precisión a los datos pero eran difíciles, si no imposibles, de interpretar en términos económicos. Los modelos VECM rompen esta dicotomía pues permiten un equilibrio entre relaciones económicas y especificaciones de series de tiempo.

Por medio de este modelo se obtuvieron así tanto las relaciones de corto como de largo plazo entre las variables de interés además se pudo analizar las funciones de impulsos y respuesta de las principales determinantes del PIB así de averiguar los potenciales cambios en ese último a partir de políticas específicas.

Finalmente se procedió también con una estimación de un modelo VAR considerando las primeras diferencias de las series de tiempo de interés. Un VAR es una estructura cuyo objetivo es modelar la persistencia en el tiempo de un vector de \(n\) series de tiempo, \(y_t\), que vienen modeladas según la siguiente especificación:

\[ y_{t}=A_{1} y_{t-1}+A_{2} y_{t-2}+\cdots+A_{p} y_{t-p}+B x_{t}+\epsilon_{t}\;\;\;(4) \]

Para cada variable del sistema se realiza automáticamente una prueba F, en la que la hipótesis nula es que ningún rezago de la variable j es significativo en la ecuación de la variable i. Esto se conoce comúnmente como prueba de causalidad de Granger.

Modelo empírico y resultados

Como previamente descrito empezamos nuestro análisis con una regresión ingenua estimada por OLS. los resultados vienen reportados en la tabla

Analizando pero visualmente las series de tiempo de nuestras variables de interés, reportadas en la gráfica siguientes, se nota que podría existir un componente de tendencia que invalidaría los supuestos del método de mínimos cuadrados.

Se procedió por lo tanto a algunos test de raíz unitaria (KPSS,ADF, ADF-GLS) para constatar si las series resultaran no estacionarios. Los resultados del ADF para las primeras diferencias respectivamente de PIB, Capital Real ajustado, Población Económicamente Activa, Gasto gubernamental, Importaciones y Exportaciones vienen aquí reportados. Podemos notar que se rechaza la hipótesis nula y por lo tanto todas las series son estacionarias en sus primeras diferencias. Los resultados del test para las variables a niveles es reportada en apéndice, para todas no se puede rechazar la hipótesis nula a un nivel de significatividad del \(5\%\). Los demás test se pueden consultar en el código y confirman los resultados estadísticos obtenidos con los ADF. Las series por lo tanto resultan todas integradas de orden 1 \(I(1)\).

Se procedió entonces a la identificación del número “óptimo” de lags que resultaron ser \(2\), como reportado en la siguiente tabla.

lags	loglik	p(LR)	AIC	BIC	HQC
1	1374.56085		-44.418695	-42.952654	-43.845246
2	1459.06822	0.00000	-46.035607	-43.312959*	-44.970630*
3	1506.87865	0.00000	-46.429288*	-42.450034	-44.872783
4	1534.33709	0.02260	-46.144570	-40.908708	-44.096536

El análisis siguió con el test de Johansen para definir el número de vectores cointegrantes.

Rank Eigenvalue Trace test	Eigenvalue	Trace test	p-value
0	0.50774	122.25	\[0.0002\]
1	0.40738	78.312	\[0.0079\]
2	0.28186	45.874	\[0.0746\]
3	0.21216	25.346	\[0.1539\]
4	0.11533	10.561	\[0.2442\]

Analizando los p-valores del test de la traza el primer renglón para el cual no se rechaza la hipótesis nula es el número \(3\). por lo tanto implementaremos un VECM con una combinación lineal de 3 variables que representará el término de corrección.

Los resultados del VECM de rango 3 con 2 lags se reportan en las siguientes tablas.

Cointegrating vectors (standard errors in parentheses)

logpib\(_{t-1}\)	1.00000	0.000000	0.000000
	(0.000000)	(0.000000)	(0.000000)
logcaprea\(_{t-1}\)	0.000000	1.00000	0.000000
	(0.000000)	(0.000000)	(0.000000)
logpea\(_{t-1}\)	0.000000	0.000000	1.00000
	(0.000000)	(0.000000)	(0.000000)
logimp\(_{t-1}\)	−0.808998	−0.729501	0.104342
	(0.110376)	(0.0983724)	(0.142211)
logexp\(_{t-1}\)	0.355114	0.811333	−0.0145863
	(0.106402)	(0.0948311)	(0.137091)
loggastpub\(_{t-1}\)	−0.388319	−1.42939	−0.902166
	(0.120083)	(0.107024)	(0.154718)

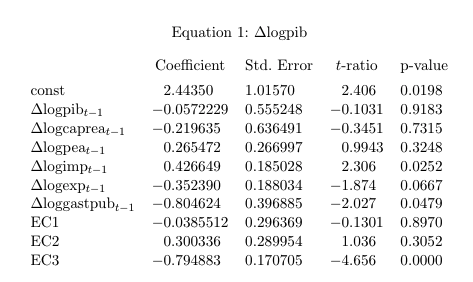
Notamos por lo tanto que la ecuación de largo plazo, por cuanto concierne la determinación del Producto Interno Bruto, tendrá la siguiente estructura:

\[ \Delta y_{t}=\mu_{0}+\Pi y_{t-1}+\sum_{i=1}^{p-1} \Gamma_{i} \Delta y_{t-i}+\epsilon_{t}\;\;\;(4) \]

Mientras la de corto plazo:

\[z_t = \beta'y_t\;\;(6)\]

Utilizando las primeras diferencias se estimó un modelo VAR para averiguar la Granger “causalidad”. Analizando la significatividad de las variables rezagadas \((l=2)\) con respecto al PIB notamos que la única significativa al \(10\%\) es la de las exportaciones. El gasto de gobierno resulta casi significativo. Considerando todas las variables en conjunto de igual forma parece haber un efecto de “causalidad” de Granger. los resultados son reportados en la siguiente tabla.

F-tests de restricciones 0

Todos los lags de d_logpib	F(2,48)=2.09024	\[0.1348\]
Todos los lags de d_logcaprea	F(2,48)=0.61733	\[0.5436\]
Todos los lags de d_logpea	F(2,48)=0.239685	\[0.7878\]
Todos los lags de d_logimp	F(2,48)=0.938968	\[0.3981\]
Todos los lags de d_logexp	F(2,48)=2.50745	\[0.0921\]
Todos los lags de d_loggastpub	F(2,48)=2.12708	\[0.1303\]
Todas las variables, lag 2	F(6,48)=1.96895	\[0.0888\]

Averiguando la relación de causalidad de “Granger” inversa con respecto a las exportaciones, como podemos notar en la siguiente tabla, la hipótesis nulas no vienen rechazadas. Por lo tanto podemos suponer que el PIB no determina las exportaciones.

F-tests de restricciones 0

Todos los lags de d_logpib	F(2,48)=0.882459	\[0.4204\]
Todos los lags de d_logcaprea	F(2,48)=0.269149	\[0.7652\]
Todos los lags de d_logpea	F(2,48)=0.478677	\[0.6225\]
Todos los lags de d_logimp	F(2,48)=1.13872	\[0.3287\]
Todos los lags de d_logexp	F(2,48)=1.74124	\[0.1862\]
Todos los lags de d_loggastpub	F(2,48)=1.20135	\[0.3097\]
Todas las variables, lag 2	F(6,48)=1.24355	\[0.3013\]

Los demás resultados de los test de causalidad de Granger son reportados en apéndice no resultan significativos.

Finalmente a partir de estos resultados analizamos las funciones impulsos y respuestas del modelo VECM por cuanto concierne las importaciones, las exportaciones y el gasto público. Los efectos a 30 trimestres vienen reportados en las siguientes figuras.

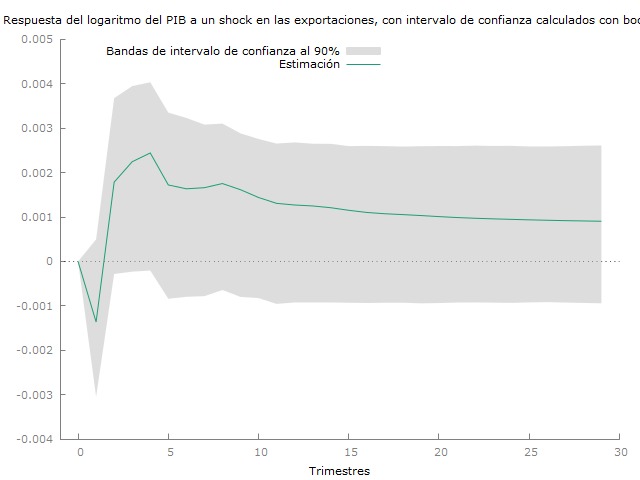
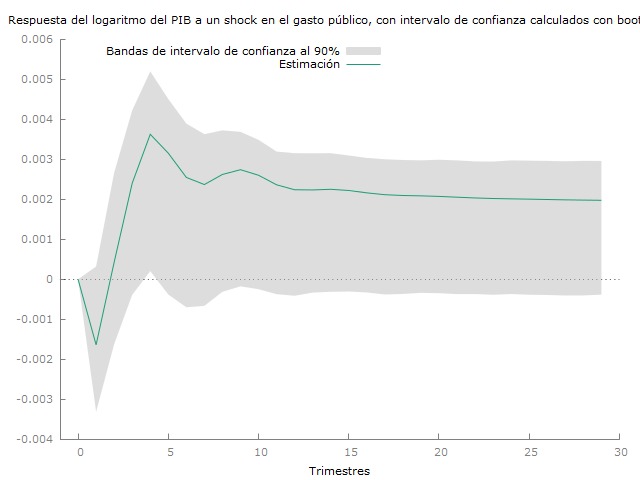
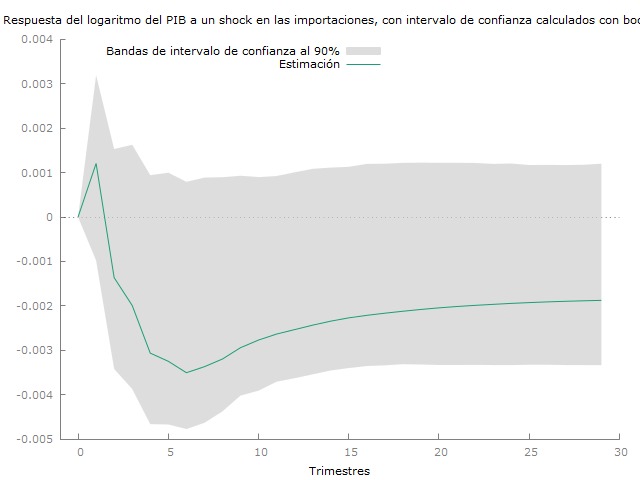Podemos notar de las funciones impulso respuesta que tanto por cuanto concierne el gasto público como por las exportaciones, un shock positivo determina un inicial disminución del PIB, pero un su aumento a largo plazo. Al contrario un aumento exógeno de las importaciones tiene el efecto contrario: un inicial aumento del PIB pero una suya disminución a largo plazo.

Por último en la siguiente figura se reportó una previsión del logaritmo del PIB para los próximos 18 años, estimado por medio del modelo VECM.

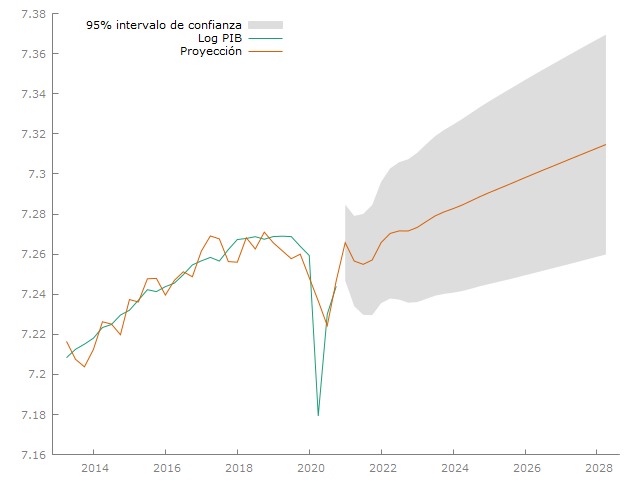
Notamos como la serie histórica es aproximada suficientemente bien por los valores ajustados del modelo VECM, aunque la crisis causada por el COVID 19 no logra un buen ajuste, probablemente por el carácter único y disruptivo desde el lado de la demanda y de la oferta de esta crisis. La proyección muestra una rápida recuperación que, pero tendrá una reversión para luego proceder con un crecimiento en un sendero estable que Se podría por lo tanto suponer que la crisis del SARS-CoV-2 determinó un quiebre estructural en el crecimiento mexicano que podría indicar un proceso de histéresis con un impacto permanente de esta crisis aún cuando este fenómeno ya se haya disipado.

Conclusiones

Notamos como la serie histórica es aproximada suficientemente bien por los valores ajustados del modelo VECM, aunque la crisis causada por el COVID 19 no logra un buen ajuste, probablemente por el carácter único y disruptivo desde el lado de la demanda y de la oferta de esta crisis. La proyección muestra una rápida recuperación que, pero tendrá una reversión para luego proceder con un crecimiento en un sendero estable que Se podría por lo tanto suponer que la crisis del SARS-CoV-2 determinó un quiebre estructural en el crecimiento mexicano que podría indicar un proceso de histéresis con un impacto permanente de esta crisis aún cuando este fenómeno ya se haya disipado.

Por cuanto concierne el modelo de determinación del crecimiento los datos de las últimas dos décadas parecen sugerir validar la hipótesis de un modelo de e crecimiento impulsado por las exportaciones (CIE). La “causalidad” de Granger mostró como los valores rezagados de las exportaciones resultan significativos estadísticamente en la determinación del PIB, mientras lo contrario no resulta verdadero. El análisis impulso respuesta muestra como un shock positivo en las exportaciones podría tener un impacto positivo a largo plazo en el crecimiento de México.

Con respecto a un aumento del gasto gubernamental, este muestra un efecto negativo en el corto plazo pero positivo a largo plazo. Las importaciones muestran mientras un comportamiento opuesto.

El análisis de las proyecciones del PIB con base en el modelo VECM parecen mostrar un quiebre estructural en el crecimiento de México causado por la crisis del COVID-19, satisfaciendo la hipótesis de histéresis de impacto permanente de la crisis económico-sanitaria en el desarrollo del país.

A partir de estas consideraciones creemos que el crecimiento mexicano, fuertemente golpeado por la crisis del SARS-CoV-2, podría recibir impulso y beneficios de un aumento en el gasto público, y el relativo abandono de la política de austeridad, y en una ulterior abertura hacía nuevo partners comerciales, fortaleciendo así las exportaciones y disminuyendo al mismo tiempo la dependencia del mercado de Estados Unidos.

Presentación

Bibliografía

[1] Robert J Barro.((Government spending in a simple model of endogeneous growth)). En:Journal ofpolitical economy98.5, Part 2 (1990), S103-S125.

[2] Sebastian Edwards.((Openness, productivity and growth: what do we really know?))En:Theeconomic journal108.447 (1998), p ́ags. 383-398.

[3] Graham Elliott, Thomas J Rothenberg y James H Stock.Efficient tests for an autoregressive unitroot. Inf. t ́ec. National Bureau of Economic Research, 1992.

[4] Elhanan Helpman y Paul R Krugman.Market structure and foreign trade: Increasing returns,imperfect competition, and the international economy. MIT press, 1985.

[5] Paul Krugman.((Import protection as export promotion)). En:H. Kierzkowslci, ed(1984).

[6] Denis Kwiatkowski y col.((Testing the null hypothesis of stationarity against the alternative of aunit root: How sure are we that economic time series have a unit root?))En:Journal of econometrics54.1-3 (1992), p ́ags. 159-178.

[7] Robert Z Lawrence y David E Weinstein.((Trade and growth: import-led or export-led? Evidencefrom Japan and Korea)). En:Rethinking the East Asian Miracle(2001), p ́ags. 379-408.

[8] Serena Ng y Pierre Perron.((Lag length selection and the construction of unit root tests with goodsize and power)). En:Econometrica69.6 (2001), p ́ags. 1519-1554.

[9] Miguel D Ramirez y Nader Nazmi.((Public investment and economic growth in Latin America: Anempirical test)). En:Review of Development Economics7.1 (2003), p ́ags. 115-126.

[10] Edmund J Sheehey.((Exports and growth: additional evidence)). En:The Journal of DevelopmentStudies28.4 (1992), p ́ags. 730-734.