Tarea 2

library(tidyverse)
library(DT) # visualizar a tablas
library(xts) # manipular series de tiempo

Problema 1

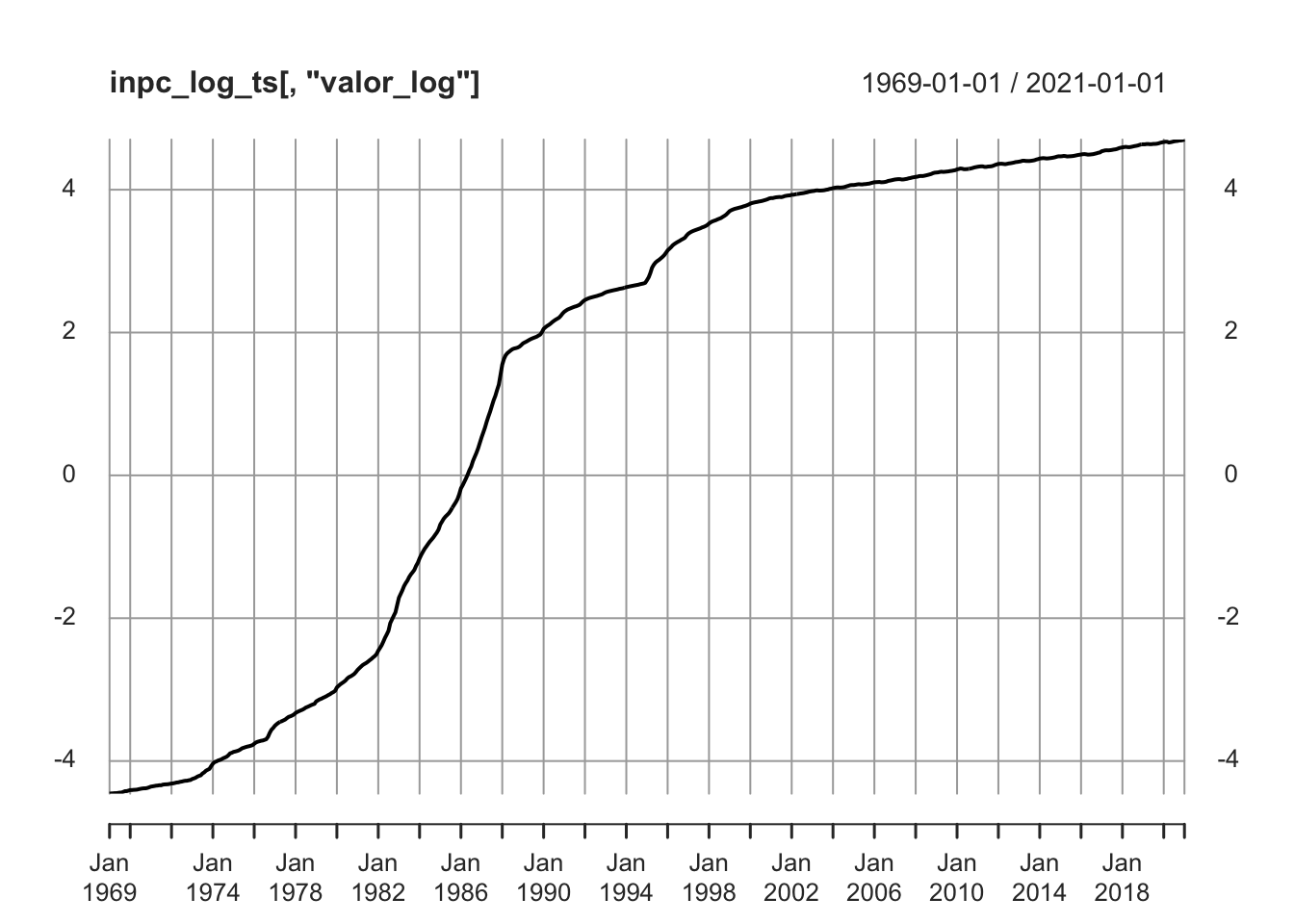
Importar la base de datos INPC como logarítmica, convertirla a serie de tiempo y graficarla (la serie comienza en enero de 1969). Descargue los datos de: https://www.inegi.org.mx/sistemas/bie/

inpc <- read_csv("Datos/BIE_T2.csv")
inpc_log <- inpc %>% mutate(valor_log = log(Valor))
datatable(inpc_log,options = list(pageLength = 12))

inpc_log_ts <- xts(inpc_log[,c("Valor","valor_log")], 
               order.by = seq(as.Date("1969-01-01"),length = nrow(inpc_log),
                              by = "month"))
plot(inpc_log_ts[,"valor_log"])

Problema 2

Problema 2a

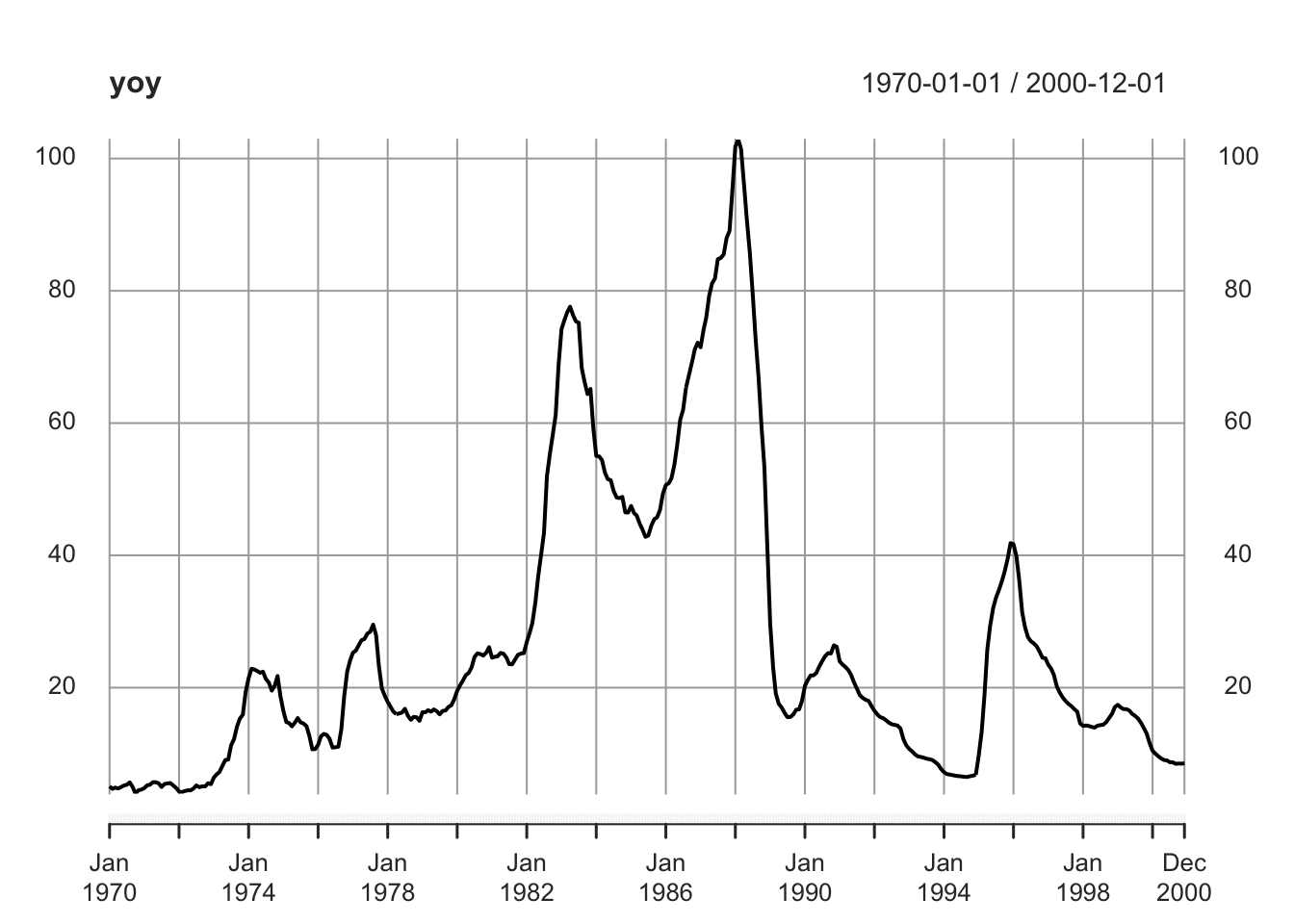
Tomar una parte de la serie de tiempo que comience en enero 1969 y termine en Diciembre 2000, calcular sus tasas anuales y convertirla a serie de tiempo

parte1 <- inpc_log_ts["197001/200012","valor_log"]
parte1_lag <- inpc_log_ts["196901/199912","valor_log"]

yoy <- (as.numeric(parte1) - as.numeric(parte1_lag))*100
yoy <- xts(x = yoy, order.by = seq(as.Date("1970-01-01"), length =NROW(yoy), by = "month"))
plot(yoy)

Problema 2b

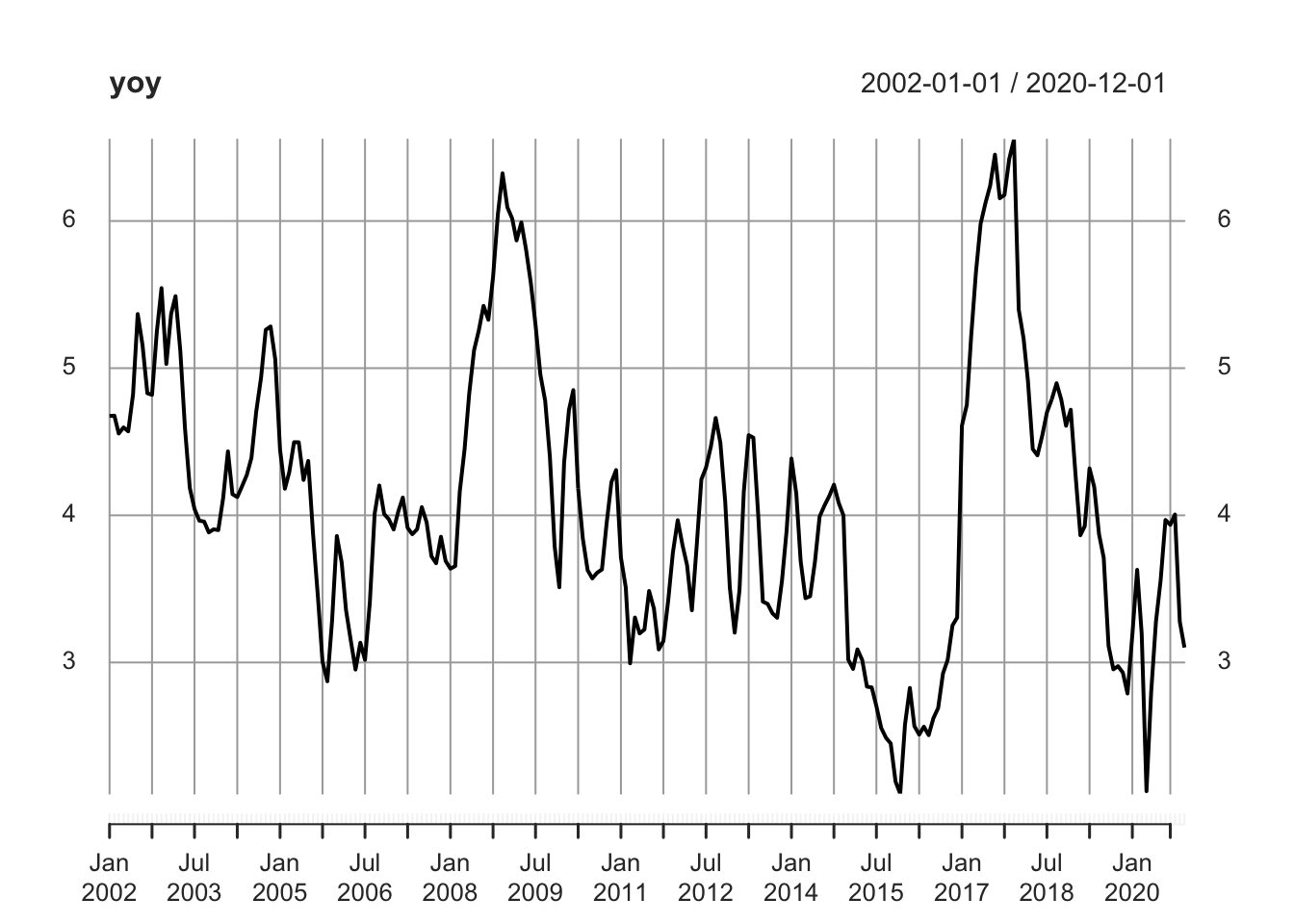
Tomar una parte de la serie de tiempo que comience en enero 2001 y termine en el año 2020, calcular sus tasas anuales y convertirla a serie de tiempo

parte2 <- inpc_log_ts["200201/202012","valor_log"]
parte2_lag <- inpc_log_ts["200101/201912","valor_log"]

yoy <- (as.numeric(parte2) - as.numeric(parte2_lag))*100
yoy <- xts(x = yoy, order.by = seq(as.Date("2002-01-01"), length =NROW(yoy), by = "month"))
plot(yoy)

Problema 2c

¿Por qué deberíamos de usar la segunda serie de tiempo (Ene 2001- Jun 2020)? Justificación económica. Ponerlo como comentario en R.

Existe bastante variación en el nivel de la tasas de la primer parte, en la decada de los 80’s y 90’s se titnen tasas de hasta 100 y 40 repectivamente. Mientras en la segunda parte de la serie, las tasas oscilan aproximadamente entre 1.5 y 7. Las comparaciones de tasas utilizando la primer parte de la serie contra datos en la segunda parte estarian sesgadas por los valores atípicos en la primer parte de la serie.

Problema 3

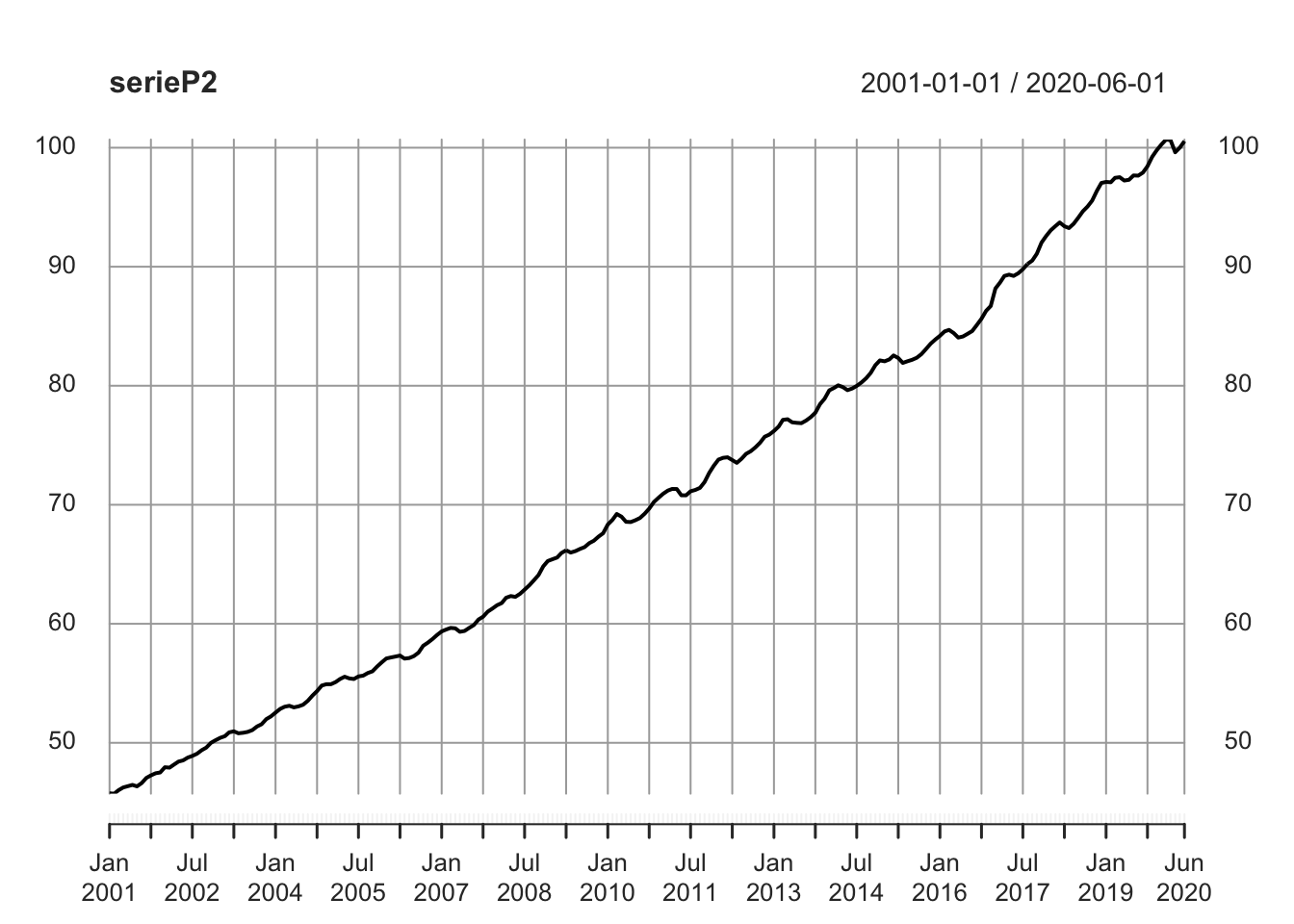
En un ciclo cambiar el año base de Julio 2018 a mayo 2020 (utilizando la serie de tiempo de Ene 2001-Jun 2020)

serieP2 <- inpc_log_ts["200101/202006","Valor"]
mayo2020 <-as.numeric(inpc_log_ts["202005","Valor"]) 
indice <- seq(as.Date("2001-01-01"), as.Date("2020-06-01"), by = "month")
for(i in indice){
  fecha <-  as.Date(i)
  serieP2[fecha,"Valor"] <- serieP2[fecha,"Valor"]/mayo2020*100
} 

Problema 3a

Grafíquela

plot(serieP2)

Problema 3b

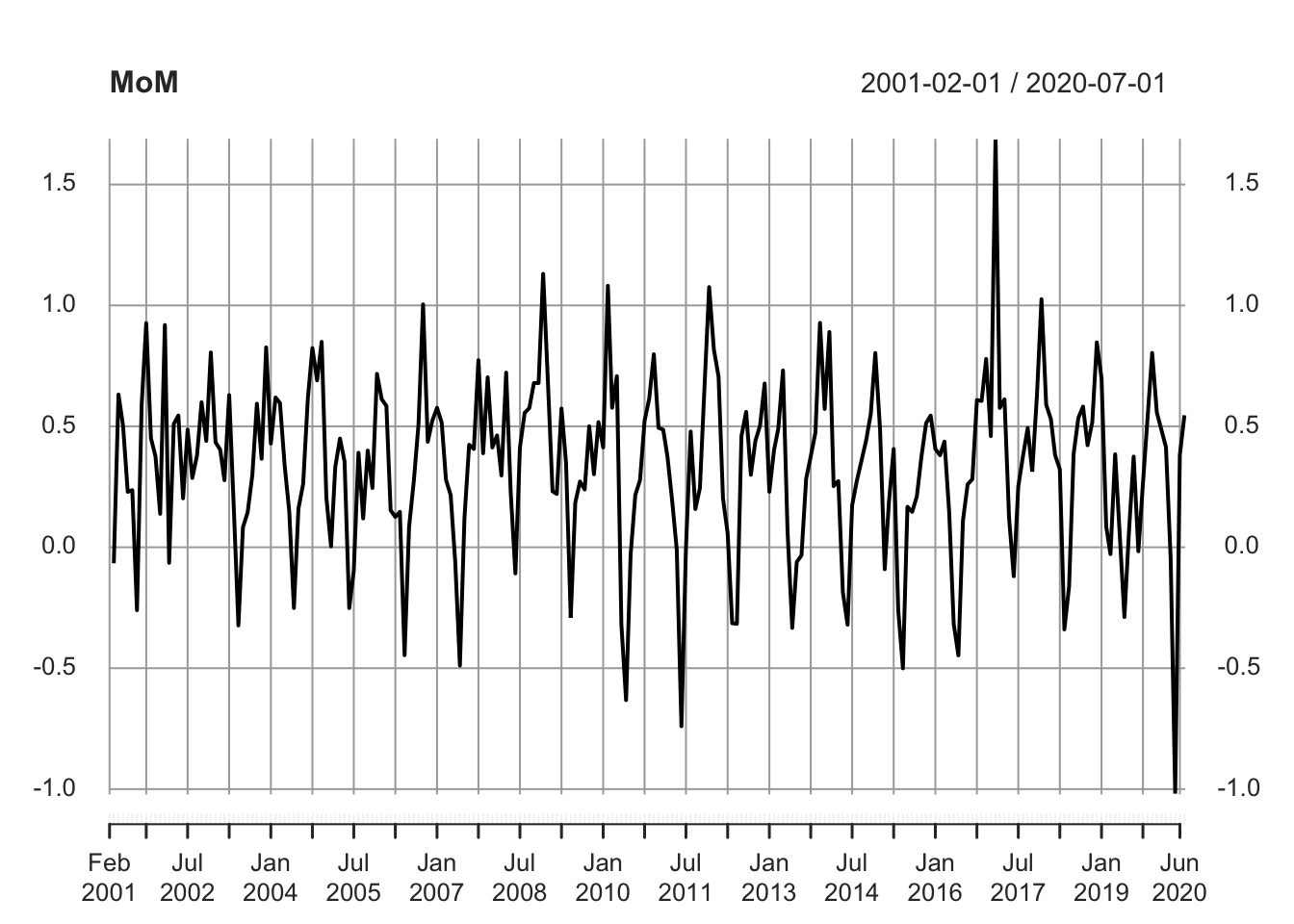
Vuelva la serie a logarítmica y calcule las tasas de crecimiento entre periodos

serieP2_log <- xts(log(as.numeric(serieP2$Valor)),
                   order.by = seq(as.Date("2001-01-01"), as.Date("2020-06-01"),
                                  by = "month")) 


MoM<-(as.numeric(serieP2_log)-lag(as.numeric(serieP2_log)))*100
MoM <- xts(x = MoM, order.by = seq(as.Date("2001-02-01"), length =NROW(MoM), by = "month"))
plot(MoM)

Problema 3c

Responda: ¿Qué tan distintas serían las tasas mensuales si se calcularán con la serie año base Julio 2018 y año base mayo 2020? Ponerlo como comentario en R

Al hacer las operaciones se tendría que tener las mismas tasas, es decir.

\[T_t = \ln(v_t*100/V_b)- \ln(v_{t-1}*100/V_b)=\ln(v_t)- \ln(v_{t-1})\]

Obsevamos que la diferencia es casi cero, salvo al aproximación computacional.

serie_log <- inpc_log_ts["200101/202006","valor_log"]

MoM1<-(as.numeric(serie_log)-lag(as.numeric(serie_log)))*100
MoM1 <- xts(x = MoM1, order.by =index(serie_log))
head(coredata(MoM1)-coredata(MoM))

##               [,1]
## [1,]            NA
## [2,]  4.440892e-14
## [3,]  0.000000e+00
## [4,] -4.440892e-14
## [5,]  0.000000e+00
## [6,]  0.000000e+00

Problema 3d

Exporta la xts a csv

write.zoo(MoM,file="Datos/tasamensual_T2.csv", sep=",")