Recursión ¶

¿Que es?¶

Muchas veces los problemas en la vida nos parecen enormes, sin duda si los descomponemos e intentamos resolver singularmente las distintas partes que los componen lograremos dirimirlos. Pico de La Mirandola (1982)

La recursión es el proceso de definir algo en termino de él mismo.
Es un concepto que se utiliza tanto en matematica como en programación
Podemos imaginarlo como dos espejos que se miran uno con el otro

En matematica la definición de recursividad es utilizada para definir unos elementos de un conjunto en terminos de otros elementos del mismo conjunto (Aczel, 1977). Algunos ejemplos de objetos que podemos definir como recursivos son la serie de Fibonacci, los numeros naturales, la serie de Fibonacci y el Conjunto de Cantor.

Una definición recursiva de una función cuando los valores de una función son dado, para algunas entradas, en terminos de los valores de la misma función dado por otras entradas (usualmente más pequeñas).

\[0!=1\]

\[(n+1)!=(n+1)n!\]

Esta definción es valida para todo numero natural \(n\) hasta llegar al caso base.

Podemos verlo haciendo el camino al revés como un proceso inductivo hasta a \(n\).

Las definición de recursión usualmente tienen dos elementos fundamentales:

el caso base
la cláusula (procedimiento) inductivo

La diferencia fundamnetal entre una definición circular y una recursiva que esta ultima siempre debe tener un caso base que satisfaga una condición sin ser definida en el procedimiento inductivo. Además el proceso inductivo debe tender hacía el caso base. De otra forma obtendriamos un regreso infinito.

Sea \(A\) un conjunto y \(a_0 \in A\). Si \(\rho\) es una función que asigna un elemento \(\rho (f) \in A\) a cada función \(f\) que mapea un subconjunto de numeros nnaturales positivos en \(A\). Entonces existe un unica función \(h:\mathbb Z_{+} \rightarrow A | h(1) =a_0 \wedge h(k) = \rho(h|S_k)\) para \(k>1\), donde \(S_k=\{ 1, \dots, k-1\}\)

Podemos por ejemplo definir la operaciones de exponente de manera recursiva como:

\[a^0=1\]

\[a^{1+n}=aa^n\]

def potenciamod(base,exp):
    if(exp==1):
        return(base)
    if(exp!=1):
        return(base*potenciamod(base,exp-1))
base=int(input("Ingresa la base: "))
exp=int(input("Ingresa el valor del exponente: "))
print("Resultado:",potenciamod(base,exp))

---------------------------------------------------------------------------
StdinNotImplementedError                  Traceback (most recent call last)
<ipython-input-1-47caf81218a4> in <module>
      4     if(exp!=1):
      5         return(base*potenciamod(base,exp-1))
----> 6 base=int(input("Ingresa la base: "))
      7 exp=int(input("Ingresa el valor del exponente: "))
      8 print("Resultado:",potenciamod(base,exp))

~/opt/anaconda3/lib/python3.8/site-packages/ipykernel/kernelbase.py in raw_input(self, prompt)
    855         """
    856         if not self._allow_stdin:
--> 857             raise StdinNotImplementedError(
    858                 "raw_input was called, but this frontend does not support input requests."
    859             )

StdinNotImplementedError: raw_input was called, but this frontend does not support input requests.

from IPython.display import IFrame, HTML, display

IFrame("http://pythontutor.com/iframe-embed.html#code=def%20potenciamod%28base,exp%29%3A%0A%20%20%20%20if%28exp%3D%3D1%29%3A%0A%20%20%20%20%20%20%20%20return%28base%29%0A%20%20%20%20if%28exp!%3D1%29%3A%0A%20%20%20%20%20%20%20%20return%28base*potenciamod%28base,exp-1%29%29%0Aprint%28%22Resultado%3A%22,potenciamod%282,4%29%29&codeDivHeight=400&codeDivWidth=350&cumulative=false&curInstr=0&heapPrimitives=nevernest&origin=opt-frontend.js&py=3&rawInputLstJSON=%5B%5D&textReferences=false",
       width =1000, height=700)

También el conjunto de numeros primos puede ser definidos como en unico conjunto de numeros positivos tales que:

1 no es un numero primo
cualquier otro entero positivo es un numero primo si y solo si no es divisible por nungún otro numero primo más pequeño que el.

def primf(num):  
    if num > 1:  
       for i in range(2,num):  
           if (num % i) == 0:  
               print(num,"No es un numero primo")  
               print(i,"x",num//i,"=",num)  
               break  
       else:  
           print(num,"Es un numero primo")
            
         
    else:  
       print(num,"No es un numero primo")
    
num = int(input("Ingresa un numero: "))      
primf(num)

Ingresa un numero: 15
15 No es un numero primo
3 x 5 = 15

IFrame("http://pythontutor.com/iframe-embed.html#code=def%20primf%28num%29%3A%20%20%0A%20%20%20%20if%20num%20%3E%201%3A%20%20%0A%20%20%20%20%20%20%20for%20i%20in%20range%282,num%29%3A%20%20%0A%20%20%20%20%20%20%20%20%20%20%20if%20%28num%20%25%20i%29%20%3D%3D%200%3A%20%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20print%28num,%22No%20es%20un%20numero%20primo%22%29%20%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20print%28i,%22x%22,num//i,%22%3D%22,num%29%20%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20break%20%20%0A%20%20%20%20%20%20%20else%3A%20%20%0A%20%20%20%20%20%20%20%20%20%20%20print%28num,%22Es%20un%20numero%20primo%22%29%0A%20%20%20%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20%20%0A%20%20%20%20else%3A%20%20%0A%20%20%20%20%20%20%20print%28num,%22No%20es%20un%20numero%20primo%22%29%0A%20%20%20%20%20%20%20%0Aprimf%2813%29%0Aprimf%2827%29&codeDivHeight=400&codeDivWidth=350&cumulative=false&curInstr=39&heapPrimitives=nevernest&origin=opt-frontend.js&py=3&rawInputLstJSON=%5B%5D&textReferences=false",
       width =1000, height=700)

def primo(n, i = 2): 
  
    # caso base 
    if (n <= 2): 
        return True if(n == 2) else False
    if (n % i == 0): 
        return False
    if (i * i > n): 
        return True 
    #proceso de itneraccion
    return primo(n, i + 1) 
  
n=int(input("Introduzca el numero: "))  
if (primo(n)): 
    print("Sí") 
else: 
    print("No") 

Introduzca el numero: 15
No

def primow(n, div = None):
    if div is None:
        div = n - 1
    while div >= 2:
        if n % div == 0:
            print("El numero no es primo")
            return True
        else:
            return primow(n, div-1)
    else:
        print("El numero es primo")
n=int(input("Enter number: "))
primow(n)

Enter number: 13
El numero es primo

IFrame("http://pythontutor.com/iframe-embed.html#code=def%20primo%28n,%20i%20%3D%202%29%3A%20%0A%20%20%0A%20%20%20%20%23%20caso%20base%20%0A%20%20%20%20if%20%28n%20%3C%3D%202%29%3A%20%0A%20%20%20%20%20%20%20%20return%20True%20if%28n%20%3D%3D%202%29%20else%20False%0A%20%20%20%20if%20%28n%20%25%20i%20%3D%3D%200%29%3A%20%0A%20%20%20%20%20%20%20%20return%20False%0A%20%20%20%20if%20%28i%20*%20i%20%3E%20n%29%3A%20%0A%20%20%20%20%20%20%20%20return%20True%20%0A%20%20%20%20%23proceso%20de%20itneraccion%0A%20%20%20%20return%20primo%28n,%20i%20%2B%201%29%20%0A%20%20%0An%3D13%0Aif%20%28primo%28n%29%29%3A%20%0A%20%20%20%20print%28%22S%C3%AD%22%29%20%0Aelse%3A%20%0A%20%20%20%20print%28%22No%22%29%20%0A%20%20%20%20%0An%3D27%0Aif%20%28primo%28n%29%29%3A%20%0A%20%20%20%20print%28%22S%C3%AD%22%29%20%0Aelse%3A%20%0A%20%20%20%20print%28%22No%22%29%20%0A&codeDivHeight=400&codeDivWidth=350&cumulative=false&curInstr=36&heapPrimitives=nevernest&origin=opt-frontend.js&py=3&rawInputLstJSON=%5B%5D&textReferences=false",
       width =1000, height=700)

IFrame("http://pythontutor.com/iframe-embed.html#code=def%20primow%28n,%20div%20%3D%20None%29%3A%0A%20%20%20%20if%20div%20is%20None%3A%0A%20%20%20%20%20%20%20%20div%20%3D%20n%20-%201%0A%20%20%20%20while%20div%20%3E%3D%202%3A%0A%20%20%20%20%20%20%20%20if%20n%20%25%20div%20%3D%3D%200%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20print%28%22El%20numero%20no%20es%20primo%22%29%0A%20%20%20%20%20%20%20%20%20%20%20%20return%20True%0A%20%20%20%20%20%20%20%20else%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20return%20primow%28n,%20div-1%29%0A%20%20%20%20else%3A%0A%20%20%20%20%20%20%20%20print%28%22El%20numero%20es%20primo%22%29%0Aprimow%2813%29%0A%0Aprimow%2827%29&codeDivHeight=400&codeDivWidth=350&cumulative=false&curInstr=74&heapPrimitives=nevernest&origin=opt-frontend.js&py=3&rawInputLstJSON=%5B%5D&textReferences=false",
       width =1000, height=700)

Después haber visto unos ejemplos podemos analizar el mecanismo a la base de este procedimiento. Sabemos que una función de python puede llamar otras funciones. Es también posible que se llame a sí misma. Esta tipologia de construcción nos permite construir el mecanismo iterativo. Analizamos desde el punto de vista de los diagramas flujo:

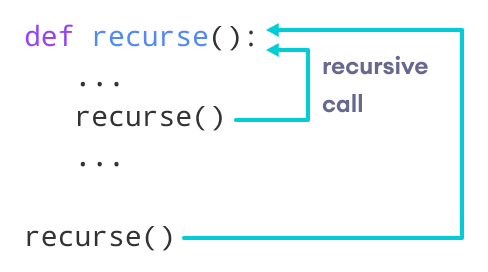
La función recurse en este caso es la función recursiva. Utilizamos este razonamiento ahora para crear una función que nos calcule el factorial de un numero \(n\)

def factorial(x):
    if x == 1:
        return 1
    else:
        return (x * factorial(x-1))


num = int(input("Ingresa un numero:"))
print("El factorial de", num, "is", factorial(num))

Ingresa un numero:5
El factorial de 5 is 120

IFrame("http://pythontutor.com/iframe-embed.html#code=def%20factorial%28x%29%3A%0A%20%20%20%20if%20x%20%3D%3D%201%3A%0A%20%20%20%20%20%20%20%20return%201%0A%20%20%20%20else%3A%0A%20%20%20%20%20%20%20%20return%20%28x%20*%20factorial%28x-1%29%29%0A%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20%0Afactorial%20%285%29&codeDivHeight=400&codeDivWidth=350&cumulative=false&curInstr=22&heapPrimitives=nevernest&origin=opt-frontend.js&py=3&rawInputLstJSON=%5B%5D&textReferences=false",
       width =1000, height=700)

Las recursiones acaban cuando alcanzams el caso base x==1.

¿Que pasaría si la función no tuviera un caso base?

Normalmente el interprete de Python define un numero maximo de recursiones para avitar loops infinitos. De default es 1000. Por lo tanto nuestro proceso se interrumpirá y nos arrojará un mensaje de error como en el ejemplo precedente.

def recursor():
    print()
    recursor()
recursor()

---------------------------------------------------------------------------
RecursionError                            Traceback (most recent call last)
<ipython-input-53-c399fc592b73> in <module>
      3     i=+1
      4     recursor(i)
----> 5 recursor(0)

<ipython-input-53-c399fc592b73> in recursor(i)
      2     print(i)
      3     i=+1
----> 4     recursor(i)
      5 recursor(0)

... last 1 frames repeated, from the frame below ...

<ipython-input-53-c399fc592b73> in recursor(i)
      2     print(i)
      3     i=+1
----> 4     recursor(i)
      5 recursor(0)

RecursionError: maximum recursion depth exceeded while calling a Python object

Ventajas y Desventajas ¶

Tenemos algunas ocasiones donde es preferible utilizar la recursión mientras otra donde puede sre más eficiente utilizar los ciclo o otra forma de codear (ej. closure)

Ventajas ¶

Podemos escribir el codigo de una manera más limpia y elegante
Un problema complejo puede ser dividida en subtareas que serán resueltas por medio de la recursividad
La generación en secuencia es más sencilla con respecto al utilizo de ciclos anidados

Desventajas ¶

Algunas veces la logíca atrás del procedimiento recursivo es dificíl de seguir e intender
Las llamadas recursivas son ineficientes para algunos problemas en cuanto necesitan mucho tiempo de elaboración y emplean mucha memoria
Hacer debugging de la funciones recursivas es más complicado, util en este caso utilizar herramientas especificas como las ofrecidas por spyder

Algunos programadores en lugar de utilizar las funciones recursivas proponen utilizar las python closure

Fuentes: Programiz w3schools Geeksforgeeks

Introducción a la ciencia de datos

Recursión¶

¿Que es?¶

Ventajas y Desventajas¶

Ventajas¶

Desventajas¶

Recursión ¶

Ventajas y Desventajas ¶

Ventajas ¶

Desventajas ¶