Contenido
Arboles de Decisiones¶
¿Qué son?¿Para que sirven?¶
Nos permiten enfrentar problemas de clasificación. Esto es un proceso de dos pasos:
Aprendizaje: se desarrolla el modelo en un conjunto de entrenamiento
Predicción: el modelo entrenado se ocupa para una predicción

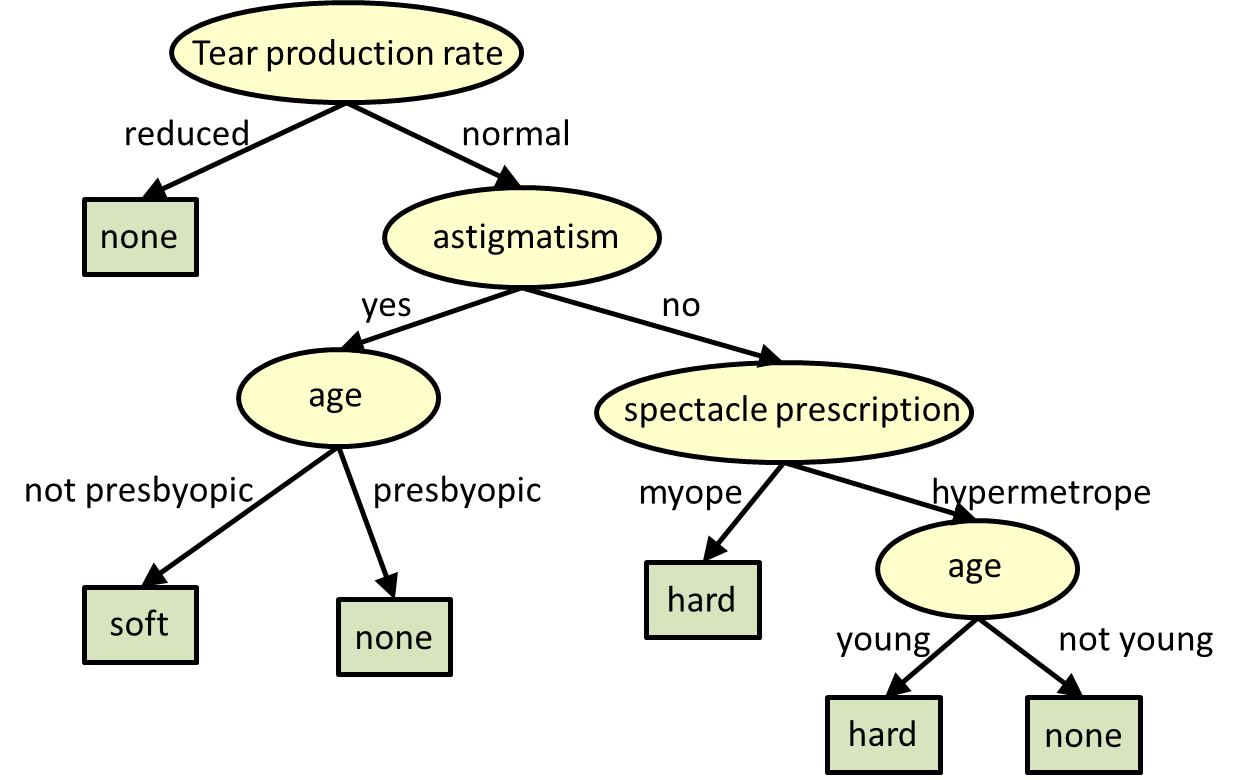
Nudo interno: rapresenta un atributo
rama: representa una decisión
hoja: representa un resultado
El nudo inciial es el nudo raíz, y de allí vamos recursivamente a partir nuestro arbol. Esta partición se hace en base a los valores de los atributos.
Pues finalmente así a veces pensamos por lo tanto son faciles de interpretar, entender y presentar.
A diferencia de otros algoritmos de ML son «white box» en cuanto nos explciitan las reglas decisionales que utilizaron (a diferencia por ejemplo de las NN)
Ventajas¶
Son faciles de interpretar y visualizar
Pueden facilmente capturar patrones no lineales
No necesitan de pre procesamiento de los datos como la normalización
Es no parametrico así no tenemos que hacer hipotesis sobre la distribución
Puede ayudarnos en la predicción de NAs y en la elección de variables
Podemos manejar problemas con alta dimensionalidad con una buena precision
su entrenamiento es más rapido con respecto a otro algoritmos como las NN
Su tiempo de elaboración dependerá del numero de caracteristicas y del numero de datos que necesitan ser procesados.
Estimamos la desigualdad con [arboles de regresión] (https://openknowledge.worldbank.org/handle/10986/29410)
Desventajas¶
Son sensibles a datos ruidosos
Poca varianza de los datos puede dar arboles diferentes. Se puede resolver por medio de bagging and boosting
Son sesgados cuando el dataset no es balanceado
Overfitting
Ensemble: tecnica de ML donde multiples modelos son entrenados utilizados el mismo algoritmo pero modificando algunos parametros para aumentar el poder predictivo.
Bagging: Se utiliza cuando el objetivo es reducir la varianza de un clasificador de árbol de decisión. Aquí el objetivo es crear varios subconjuntos de datos a partir de la muestra de entrenamiento elegida al azar con reemplazo. Cada recopilación de datos de subconjuntos se utiliza para entrenar sus árboles de decisión. Como resultado, obtenemos un conjunto de diferentes modelos. Se utiliza el promedio de todas las predicciones de diferentes árboles, que es más robusto que un clasificador de árbol de decisión único.
Boosting: Los árboles consecutivos se ajustan en cada paso, el objetivo es mejorar la precisión del árbol anterior. Cuando una entrada se clasifica erróneamente por una hipótesis, su peso se incrementa para que sea más probable que la siguiente hipótesis la clasifique correctamente.

¿ Cómo funcionan?¶
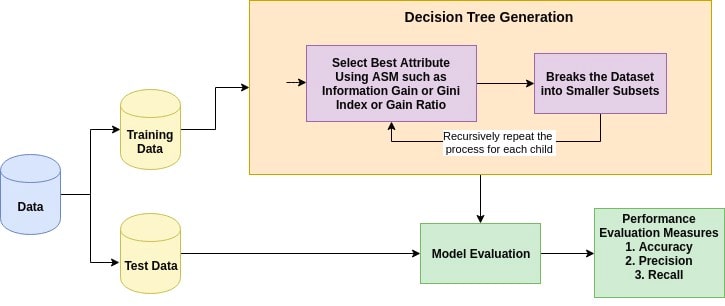
La idea basica es la siguiente:
Se selecciona el mejor atributo utilizando ASM (Misura de Selección de los Atributos) para dividir las observaciones
Este atributo se utiliza como nudo de decisión y se divide el conjunto en subconjuntos
Se sigue repitiendo el procedimiento hasta que:
No hay más atributos
No hay más casos
No hay más varianza, todos los record rimanentes tienen el mismo valor del atributo
Se alcanza la profundidad maxima del arbol
Seleccion de atributos¶
La medida de selección de un atgributo es una heuristíca oara seleccionar el criterio de partición de kis datos de la mejor manera posibles. Se define también como regla de partición.
Nos da una clasificación para cada atributo.
El atributo que logra el mejor puntaje es utilizado para la partición.
Los criterios más famosos son el criterio de ganancia de información, la razón de ganancia y el indice de Gini
Ganancia de información¶
Se basa en el concpeto de entropia que mide la «impuridad» de un conjunto. En teoria de la información se refiere a la impureza del grupo examinado. La ganancia de información es representado por el decrecimiento de la entropia. Se calcula con base a la entrepia antes de la división y la entropia promedia despues de la subdivison con base a algun atributo especifico. El algoritmo de árbol de decisión ID3 (dicotomizador iterativo) utiliza la ganancia de información:
Con \(p_i\) es la probabilidad que una observación cualquiera en \(D\) pertenezca a la clase \(C_i\).
El atributo \(A\) que tiene el mayor aumento de ganacia es utilizado para efectuar la partición.
Razón de Ganancia¶
Usalmente GI es sesgado siendo que prefiere el atribusto con un mayor numero de valores distintos. Por ejemplo el ID, maximiza el GI.
Con la RG se resuelve el sesgo normalizando la GI utilizando la información de la partición (Split Info)
Indice de Gini¶
Considera una partición binaria de cada atributo. Podemos por lo tnato calcular una media pesada de la impurez de cada partición.
En caso de atributos discretos se considera el subconjunto que minimiza el indice, en caso de atributo continuo se selcciona cada pareja de puntos adiacientes como uin posible punto de division
El atributo con el minimo valor de Gini es elegido como atributo para la partición.
import matplotlib as plt
from sklearn.datasets import load_iris
from sklearn import tree
X, y = load_iris(return_X_y=True)
clf = tree.DecisionTreeClassifier()
clf = clf.fit(X, y)
X
iris=load_iris(as_frame=True)
iris
{'data': sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
.. ... ... ... ...
145 6.7 3.0 5.2 2.3
146 6.3 2.5 5.0 1.9
147 6.5 3.0 5.2 2.0
148 6.2 3.4 5.4 2.3
149 5.9 3.0 5.1 1.8
[150 rows x 4 columns],
'target': 0 0
1 0
2 0
3 0
4 0
..
145 2
146 2
147 2
148 2
149 2
Name: target, Length: 150, dtype: int64,
'frame': sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) \
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
.. ... ... ... ...
145 6.7 3.0 5.2 2.3
146 6.3 2.5 5.0 1.9
147 6.5 3.0 5.2 2.0
148 6.2 3.4 5.4 2.3
149 5.9 3.0 5.1 1.8
target
0 0
1 0
2 0
3 0
4 0
.. ...
145 2
146 2
147 2
148 2
149 2
[150 rows x 5 columns],
'target_names': array(['setosa', 'versicolor', 'virginica'], dtype='<U10'),
'DESCR': '.. _iris_dataset:\n\nIris plants dataset\n--------------------\n\n**Data Set Characteristics:**\n\n :Number of Instances: 150 (50 in each of three classes)\n :Number of Attributes: 4 numeric, predictive attributes and the class\n :Attribute Information:\n - sepal length in cm\n - sepal width in cm\n - petal length in cm\n - petal width in cm\n - class:\n - Iris-Setosa\n - Iris-Versicolour\n - Iris-Virginica\n \n :Summary Statistics:\n\n ============== ==== ==== ======= ===== ====================\n Min Max Mean SD Class Correlation\n ============== ==== ==== ======= ===== ====================\n sepal length: 4.3 7.9 5.84 0.83 0.7826\n sepal width: 2.0 4.4 3.05 0.43 -0.4194\n petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)\n petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)\n ============== ==== ==== ======= ===== ====================\n\n :Missing Attribute Values: None\n :Class Distribution: 33.3% for each of 3 classes.\n :Creator: R.A. Fisher\n :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)\n :Date: July, 1988\n\nThe famous Iris database, first used by Sir R.A. Fisher. The dataset is taken\nfrom Fisher\'s paper. Note that it\'s the same as in R, but not as in the UCI\nMachine Learning Repository, which has two wrong data points.\n\nThis is perhaps the best known database to be found in the\npattern recognition literature. Fisher\'s paper is a classic in the field and\nis referenced frequently to this day. (See Duda & Hart, for example.) The\ndata set contains 3 classes of 50 instances each, where each class refers to a\ntype of iris plant. One class is linearly separable from the other 2; the\nlatter are NOT linearly separable from each other.\n\n.. topic:: References\n\n - Fisher, R.A. "The use of multiple measurements in taxonomic problems"\n Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to\n Mathematical Statistics" (John Wiley, NY, 1950).\n - Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.\n (Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.\n - Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System\n Structure and Classification Rule for Recognition in Partially Exposed\n Environments". IEEE Transactions on Pattern Analysis and Machine\n Intelligence, Vol. PAMI-2, No. 1, 67-71.\n - Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule". IEEE Transactions\n on Information Theory, May 1972, 431-433.\n - See also: 1988 MLC Proceedings, 54-64. Cheeseman et al"s AUTOCLASS II\n conceptual clustering system finds 3 classes in the data.\n - Many, many more ...',
'feature_names': ['sepal length (cm)',
'sepal width (cm)',
'petal length (cm)',
'petal width (cm)'],
'filename': '/Users/rafamtz/opt/anaconda3/lib/python3.8/site-packages/sklearn/datasets/data/iris.csv'}
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, plot_tree
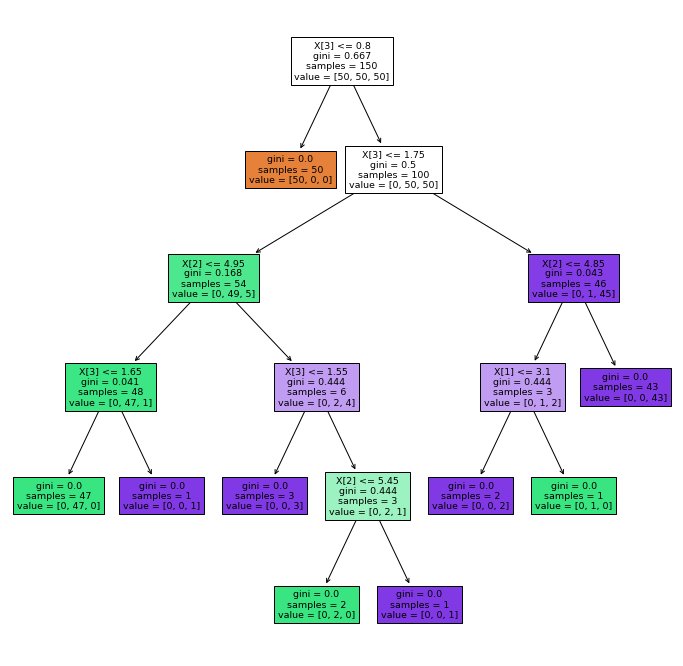
plt.figure(figsize=(12,12))
tree.plot_tree(clf, filled=True)
plt.show()
Los algoritmos de aprendizaje automático de clasificación aprenden a asignar etiquetas a los ejemplos que le damos como input.
Las caracteristica de input representan un espacio de entrada continuo.
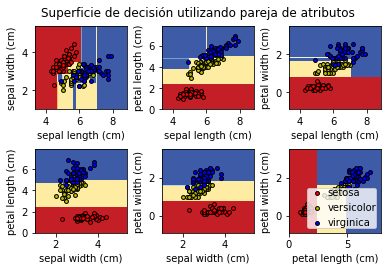
Podemos pensar en cada característica de entrada definiendo un eje o dimensión en un espacio de características. Dos entradas definen un espacio de observaciones que es un plano, con puntos que representan las coordenadas de entrada en el espacio de entrada. Si hubiera tres variables de entrada, el espacio de características sería un volumen tridimensional.
A cada punto del espacio se le puede asignar una etiqueta de clase. Esto lo representamos por medio de distintos colores.
El objetivo de un algoritmo de clasificación es aprender a dividir el espacio de características de modo que las etiquetas se asignen correctamente a los puntos en el espacio de características, o al menos, lo más correctamente posible.
Esta es una comprensión geométrica útil del modelado predictivo de clasificación.
Una vez que un algoritmo de aprendizaje automático de clasificación divide un espacio de características, podemos clasificar cada punto en el espacio de características, en alguna cuadrícula arbitraria, para tener una idea de cómo exactamente el algoritmo eligió dividir el espacio de características.
Esto se denomina superficie de decisión o límite de decisión y proporciona una herramienta de diagnóstico para comprender un modelo en una tarea de modelado predictivo de clasificación.
Aunque la noción de «superficie» sugiere un espacio de características bidimensional, el método se puede utilizar con espacios de características con más de dos dimensiones, donde se crea una superficie para cada par de características de entrada.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, plot_tree
# Parameters
n_classes = 3
plot_colors = "ryb"
plot_step = 0.02
# Load data
iris = load_iris()
for pairidx, pair in enumerate([[0, 1], [0, 2], [0, 3],
[1, 2], [1, 3], [2, 3]]):
# We only take the two corresponding features
X = iris.data[:, pair]
y = iris.target
# Train
clf = DecisionTreeClassifier().fit(X, y)
# Plot the decision boundary
plt.subplot(2, 3, pairidx + 1)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, plot_step),
np.arange(y_min, y_max, plot_step))
plt.tight_layout(h_pad=0.5, w_pad=0.5, pad=2.5)
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
cs = plt.contourf(xx, yy, Z, cmap=plt.cm.RdYlBu)
plt.xlabel(iris.feature_names[pair[0]])
plt.ylabel(iris.feature_names[pair[1]])
# Plot the training points
for i, color in zip(range(n_classes), plot_colors):
idx = np.where(y == i)
plt.scatter(X[idx, 0], X[idx, 1], c=color, label=iris.target_names[i],
cmap=plt.cm.RdYlBu, edgecolor='black', s=15)
plt.suptitle("Superficie de decisión utilizando pareja de atributos")
plt.legend(loc='lower right', borderpad=0, handletextpad=0)
plt.axis("tight")
plt.show()