Contenido

Estructuras

  • Tipos númericos, int (> bool) (no mutable), float (no mutable), complex.

iterable. Un objeto capaz de devolver sus miembros uno a la vez.

secuencia. Un iterable que logra un acceso eficiente a los elementos usando índices enteros.

contenedor. Un objeto que hace referencias a otros objetos (ejemplo: tuplas, listas, diccionarios)

hashable. Un objeto es hashable si tiene un valor de hash (por ejemplo: posición de los elementos de las tuplas) que nunca cambiará durante su tiempo de vida

  • Tipo conjunto, set (mutable), frozenset. Un objeto de tipo conjunto o set es una colección no ordenada de distintos objetos hashables.

  • …

  • Tipo Mapeo, dict (mutable). Un objeto de tipo mapping relaciona valores (que deben ser hashable) con objetos de cualquier tipo.

Para saber más: Solución de problemas con algoritmos y estructuras de datos usando Python

Tarea moral: ¿Qué es/hace id?, ¿Qué es/hace zip?

dir(tuple)

['__add__',
 '__class__',
 '__contains__',
 '__delattr__',
 '__dir__',
 '__doc__',
 '__eq__',
 '__format__',
 '__ge__',
 '__getattribute__',
 '__getitem__',
 '__getnewargs__',
 '__gt__',
 '__hash__',
 '__init__',
 '__init_subclass__',
 '__iter__',
 '__le__',
 '__len__',
 '__lt__',
 '__mul__',
 '__ne__',
 '__new__',
 '__reduce__',
 '__reduce_ex__',
 '__repr__',
 '__rmul__',
 '__setattr__',
 '__sizeof__',
 '__str__',
 '__subclasshook__',
 'count',
 'index']

L = [1,2]
a = (L,3)

print(a)
L[1]= "a"
print(a)

([1, 2], 3)
([1, 'a'], 3)

dir(set)

['__and__',
 '__class__',
 '__contains__',
 '__delattr__',
 '__dir__',
 '__doc__',
 '__eq__',
 '__format__',
 '__ge__',
 '__getattribute__',
 '__gt__',
 '__hash__',
 '__iand__',
 '__init__',
 '__init_subclass__',
 '__ior__',
 '__isub__',
 '__iter__',
 '__ixor__',
 '__le__',
 '__len__',
 '__lt__',
 '__ne__',
 '__new__',
 '__or__',
 '__rand__',
 '__reduce__',
 '__reduce_ex__',
 '__repr__',
 '__ror__',
 '__rsub__',
 '__rxor__',
 '__setattr__',
 '__sizeof__',
 '__str__',
 '__sub__',
 '__subclasshook__',
 '__xor__',
 'add',
 'clear',
 'copy',
 'difference',
 'difference_update',
 'discard',
 'intersection',
 'intersection_update',
 'isdisjoint',
 'issubset',
 'issuperset',
 'pop',
 'remove',
 'symmetric_difference',
 'symmetric_difference_update',
 'union',
 'update']

help(set.issubset)

Help on method_descriptor:

issubset(...)
    Report whether another set contains this set.

dir(dict)

['__class__',
 '__contains__',
 '__delattr__',
 '__delitem__',
 '__dir__',
 '__doc__',
 '__eq__',
 '__format__',
 '__ge__',
 '__getattribute__',
 '__getitem__',
 '__gt__',
 '__hash__',
 '__init__',
 '__init_subclass__',
 '__iter__',
 '__le__',
 '__len__',
 '__lt__',
 '__ne__',
 '__new__',
 '__reduce__',
 '__reduce_ex__',
 '__repr__',
 '__reversed__',
 '__setattr__',
 '__setitem__',
 '__sizeof__',
 '__str__',
 '__subclasshook__',
 'clear',
 'copy',
 'fromkeys',
 'get',
 'items',
 'keys',
 'pop',
 'popitem',
 'setdefault',
 'update',
 'values']

a = dict(one=1, two=2, three=3)
b = {'one': 1, 'two': 2, 'three': 3}
c = dict(zip(['one', 'two', 'three'], [1, 2, 3]))
d = dict([('two', 2), ('one', 1), ('three', 3)])
e = dict({'three': 3, 'one': 1, 'two': 2})
f = dict({'one': 1, 'three': 3}, two=2)
a == b == c == d == e == f

True

Ejemplos

Fracciones:

Puedes expresar una fracción como una tupla: (numerador, denominador).

a). Escribe una función que sume dos fracciones que sus argumentos sean tuplas

b). Escribe una función que multiplique dos fracciones que sus argumentos sean tuplas

Apéndice

Módulo: sympy

Existe un módulo para realizar operaciones matemáticas simbólicas: sympy

import sympy

# dir(sympy)
x = sympy.symbols('x')
f = sympy.sin(x)
fp = sympy.diff(f, x, 2)
fp.subs(x, 3)
\[\displaystyle - \sin{\left(3 \right)}\]

Si queremos implementar un programa que encuentre el polinomio \(n\) de Taylor de la función \(f\) en el punto \(x_0\)

\[P_n(x) = \sum_{i=0}^n \frac{f^{(i)}(x_0)}{i!}(x-x_0)^i = f(x_0) + f^{(1)}(x_0)(x-x_0)+ \frac{f^{(2)}(x_0)}{2!}(x-x_0)^2 + \dots +\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n \]
def taylor(f,x,x0,n):
    if n == 0:
        return f.subs(x, x0)
    else:
        return sympy.diff(f,x,n).subs(x,x0)/sympy.factorial(n) * (x - x0) ** n + taylor(f,x,x0,n-1)

g = sympy.exp(x)

x0 = sympy.symbols('x_0')

gt = taylor(g, x, 1, 3)
gt
\[\displaystyle \frac{e \left(x - 1\right)^{3}}{6} + \frac{e \left(x - 1\right)^{2}}{2} + e \left(x - 1\right) + e\]
p1 = sympy.plot(g, gt, xlim = (-2, 2), ylim = (-1,10), show = False)
p1.show()
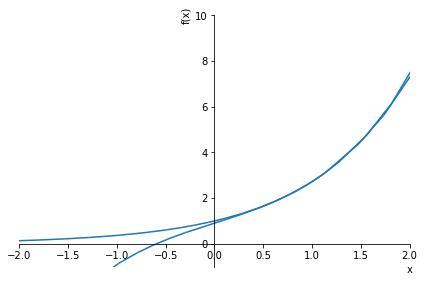
../../_images/Estructuras_15_0.png

Tambien puede resolver ecuaciones diferenciales

import sympy as sym

t = sym.symbols('t')
y = sym.Function('y')(t)
lie = y.diff(t,2) +  9*y
expr = sym.Eq(lie, sym.sin(t))
expr
\[\displaystyle 9 y{\left(t \right)} + \frac{d^{2}}{d t^{2}} y{\left(t \right)} = \sin{\left(t \right)}\]
sym.dsolve(expr)
\[\displaystyle y{\left(t \right)} = C_{1} \sin{\left(3 t \right)} + C_{2} \cos{\left(3 t \right)} + \frac{\sin{\left(t \right)}}{8}\]

Crear módulos

Pordemos crcear módulos para utilizarlos en diferentes programas. Existe una documentación para hacer un módulo y que este se pueda compartir con cualquier usuario (algo asi como conda install mi_modulo_que_comparti), aquí solo veremos la implemenación local. Si te interesa aprender sobre como crear módulos puedes concultar el sigeuiente enlace

import mimodulo as m

import sympy

x = sympy.symbols('x')
g = sympy.exp(x)

gt = m.taylor(g, x, 1, 3)
gt
\[\displaystyle \frac{e \left(x - 1\right)^{3}}{6} + \frac{e \left(x - 1\right)^{2}}{2} + e \left(x - 1\right) + e\]
import ipywidgets as widgets
a = widgets.IntSlider()
widgets.interact(lambda n: m.taylor(g,x,1,n), n =2)

<function __main__.<lambda>(n)>
Arboles de Decisiones Laboratorio 7